圆锥曲线知识初次传入是在明末清初。李俨先生的《中算家的圆锥曲线说》首次论述了这一阶段圆锥曲线知识传入中国的大概情形^[8]，牛亚华的《明末清初椭圆知识的传入及应用》在李俨先生研究的基础上，进一步挖掘和整理史料，对这一阶段进行了较全面而又细致的论述^[9]。本节参考前人的研究成果，对此阶段传入的圆锥曲线知识进行简要介绍和论述。

明末清初，随着耶稣会传教士来华，西方的天文、数学等科学知识传入中国。圆锥曲线知识也是在这时首次被介绍到中国。在早期传入的圆锥曲线知识中，以椭圆知识为主，也只有椭圆知识得到中算家的重视，应用较多。从时间上说，可以分为17世纪和18世纪两个阶段。前一阶段传入的椭圆知识主要保存在天文、机械、力学等著作中，如《崇祯历书》《灵台仪象志》《远西奇器图说》等书均有这方面的内容。后一阶段以《数理精蕴》（1723年）和《历象考成后编》（1742年）为主。

《崇祯历书》是一部卷帙浩繁的天文历算综合性著作，共137 卷，涉及椭圆知识的主要有《测量全义》（1631年）、《恒星历指》（1631年）、《交食历指》（1632年）、《测天约说》（1633年）。因为这些都是历算书籍，对于圆锥曲线的论说既不详细，也不完备，译名也不统一。如椭圆，《测量全义》称为椭圆形；《恒星历指》称为椭圆，也称为斜圆；《交食历指》则称为长圆，《测天约说》上卷“测量学”第一题记为：“长圆者，一作圈，而首至尾之径大于腰间径。亦名曰瘦圈界，亦名椭圆。”

《测量全义》介绍的椭圆知识较多，包括椭圆的形成方法、椭圆面积公式、旋转体体积及部分体积公式。

卷四“测面（上）”中的“界说”介绍了椭圆的另一种形成方法——通过斜截圆柱体得到，认为“椭圆，如圆柱而斜剡之，得两面焉”。后来中算家一般都接受了这一说法。

卷五“测面（下）”详细介绍说：“量椭圆法。椭圆形者，斜截圆柱所成两面形也。”紧接着指出椭圆

形有长短二径。古士默徳本论曰：两径之中比例线为径作圈与椭圆等，则两径为第一、第三率，相乘所得方数为第二率；又同线上之正方与圈容为一四与一一。今两率相乘者，即中率正方之数，故以两径相乘得数，以一一乘之，以一四除之，得椭圆之积也。^[10]

“古士默徳”即古希腊的阿基米德，他曾用双归谬法证明了椭圆面积等于以长短两半径积的平方根为直径的圆的面积，这个圆称为中率圆，即S椭圆=S中率圆。中率圆的外切正方形的面积为S方=长轴×短轴，它们的面积比为S中率圆：S方=11：14，其中圆周率取π=。这段文字相当于给出了椭圆的面积公式：S椭圆=S中率圆==长轴×短轴=长轴×短轴。

卷六“测体”介绍了利用平面切割圆锥体的方法得到圆锥曲线的方法，内容如下（括号内为原文双行小字注释）。

截圆角体法有五。从其轴，平分直截之，所截两面为三角形，一也。横截之，与底平行，截面为平圆形，二也。斜截之，与边平行截面为圭窦形（顶不锐，近底之两腰稍平行），三也。直截之，与轴平行，截面为陶丘形（顶曲，渐下渐直，底两旁为锐角），四也。无平行，任斜截之，截面为椭圆形，五也。

此即由于平面于圆锥底面夹角的不同，得到五种截面：三角形、平圆形、圭窦形（抛物线）、陶丘形（双曲线）、椭圆形。文中还给出了示意图。

《交食历指》卷七“以长圆形求日食方法”节，称“正对太阳其景（影）必圆，今以斜对之平面，亦在密室中受景（影），孔仍如前小，则所得形必长圆”，此处“长圆”即椭圆，此节还介绍了椭圆作法及椭圆基本定理。

南怀仁（Ferdinard Verbiest，1623—1688年）的《灵台仪象志》（1674年）全书共16 卷，是为说明当时新制的几件天文仪器的结构、原理、安装以及使用方法而撰写的，后两卷全部为插图，共117 幅图，其中第16、55、59、117 等4 幅图涉及圆锥三曲线。第16 和第55 两图图示了椭圆的拉线画法，第55 图还给出了椭圆规的结构图。如图1-2-1，丁字尺上刻有互相垂直的槽，在另一直尺上固定两颗钉，将这两颗钉分别置于纵横槽中，让钉在槽中运动，则直尺末端的笔就可绘出一椭圆曲线。由于是丁字尺，所画椭圆是半椭圆。后来，李善兰在《椭圆拾遗》中对这一椭圆规的原理给出了证明。第59 图中有椭圆和双曲线的拉线画法的图示。第117 图图示了从两种火器发射的子弹的弹道轨迹，明显是抛物线（如图1-2-2）。

(www.daowen.com)

图1-2-1　《灵台仪象志·图》第55 图（部分）

以上是17世纪传入中国椭圆知识的大概情形，虽不够系统和全面，但均为新的数学内容，很多为中国人首次知晓。

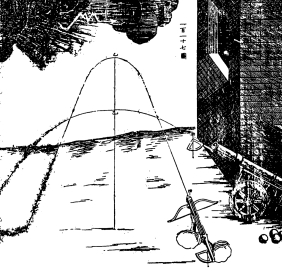
图1-2-2　《灵台仪象志·图》第117 图

《数理精蕴》上编卷三“几何原本·八·第十二”证明了椭圆的面积公式，其方法是利用椭圆与大辅圆的关系，它称：

凡圆面径与椭圆面高度等者，其面积互相为比之比例，即同于函两形各作切方形互相为比之比例。而圆形面积与椭圆形面积互相为比之比例，又同于圆形径与椭圆形小径互相为比之比例也。

即认为椭圆与大辅圆的面积之比等于椭圆外切长方形面积与大辅圆外切正方形面积之比，还等于圆径与椭圆短径之比。这个方法与之前《测量全义》所介绍的不同。

上编卷三“几何原本·十·第十二”利用卡瓦列里原理证明了旋转椭球体的体积公式^[11]，它称：“凡椭圆体大径与圆球体径相等者，其二体积之比例，即同与椭圆体小径所作方面与圆球体径所作方面之比例也。”证明主要认为这个比例等于“将椭圆体与球体任意依径线平行分之，其所分之大小平圆面”之比例。

上编卷三“几何原本·十·第十五”还对旋转椭球体的表面积进行探讨，但结论不正确。此外，还给出椭台体体积的三种解法。

《历象考成后编》是由明安图等人于乾隆二年（1737年）开始编纂，五年后编成。该书引入了颠倒的行星运动的椭圆模型，涉及椭圆的一些算法，主要是针对椭圆轨道运动。此书的编纂背景以及椭圆轨道运动的算法将在第二章详细论述。

以上就是明末清初圆锥曲线初次传入中国的大体情况，总的来说，因为大部分是随着历算书籍传入，圆锥曲线的论说不详细，也不完备，其中主要以椭圆知识为主。从数学角度而言，主要有四项内容：椭圆基本定理、面积公式、椭圆切线定理以及行星运动的椭圆算法。

圆锥曲线传入后中算家随之对它们展开了研究。主要是两方面：椭圆轨道问题推算以及椭圆求周术的研究，以焦循、项名达、徐有壬、李善兰等人的工作为代表，在第二章和第三章我们将详细论述。