1.圆锥曲线研究的起源

圆锥曲线的研究，起源于古希腊，它与几何三大作图问题中的倍立方问题有关^[2]，该问题指的是要用尺规作图的方法求作一立方体使其体积等于已知立方体的两倍。公元前5世纪，古希腊数学家希波克拉底（Hippocrates，公元前5世纪）指出倍立方问题可以归结为在一线段与另一双倍长的线段之间求两个比例中项的问题，即求二次比的问题。用现在的代数符号来表示，令x和y 是这样两个量，使得

a：x=x：y=y：2a

则

x2=ay，y2=2ax，xy=2a2

由前两式可以得到

x3=2a3

得到x 便解决了倍立方问题，但它不能用尺规作出。从解析几何而言，x和y 就是两条抛物线的交点或一抛物线和一双曲线的交点的坐标。^[3]几何三大问题曾轰动一时，讨论者很多，曾研究过倍立方问题的著名希腊学者还有阿契塔（Archytas，约公元前428 至前347年）、柏拉图（Plato，约公元前427至前347年）、欧多克斯（Eudoxus，约公元前408 至前355年）及梅内克缪斯（Meneachmus，约公元前375 至前325年）等。

梅内克缪斯的方法可能是之前研究的总汇。他取三个正圆锥，一为直角，一为锐角，一为钝角，各作一平面垂直于一条母线，并与圆锥相截，称截线分别为“直角圆锥截线”“锐角圆锥截线”“钝角圆锥截线”（即今之抛物线、椭圆、等轴双曲线一支），这是最早的对圆锥曲线的命名。他用两条抛物线或一抛物线与一双曲线的交点解决倍立方问题。梅内克缪斯的著作早已散失，根据后来学者考证，以“直角圆锥截线”（抛物线）的方法为例说明如下：

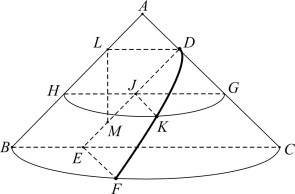
图1-1-1

如图1-1-1，RtΔBAC 是直角圆锥的轴截面，截面DEF 垂直于母线AC，交轴截面于DE。在DE 上任取一点J，过J 点作正截面HKG，与DEF交于JK，作DL∥HG，LM ⊥LD 交DE于M 点。于是有

JK2=HJ·GJ=LD·JG=JD·DM

若设x=JD，y=JK，p=DM，则有

y2=px

显然这就是抛物线的方程。

同样，能得到“锐角圆锥截线”“钝角圆锥截线”。这就是圆锥三曲线的起源研究——所谓的“梅内克缪斯三曲线”。

2.阿波罗尼奥斯的《圆锥曲线论》(www.daowen.com)

梅内克缪斯之后不久，研究圆锥曲线的学者比较著名的有欧几里得（Euclid，约公元前300年）、阿基米德（Archimedes，约公元前287 至前212年）、阿波罗尼奥斯。

欧几里得有本著作为《圆锥割线》（Conics），根据帕普斯的说法，这部失传的著作共含四篇，后来被阿波罗尼奥斯引用，成为其《圆锥曲线论》的头三篇的主要内容。欧几里得把圆锥曲线分为三类不同的圆锥的割线来处理。椭圆可任由一圆锥或一圆柱的割线得到。阿基米德圆锥曲线研究的重要成就就是利用穷竭法得出抛物线弓形面积，他还发明圆锥曲线的直径。

最主要的是阿波罗尼奥斯的研究，他的《圆锥曲线论》（Conic Sections）可以看成圆锥曲线论创立的标志。《圆锥曲线论》共8 卷，末卷遗失。卷1 论三种曲线的产生，卷2 论渐近线、轴及直径，卷3 论三种曲线的轨迹问题，卷4 论直线的调和分割，两曲线不多于四个交点，两曲线的位置关系，卷5论极大与极小值问题，卷6 论相似圆锥曲线，卷7 论共轭直径，卷8 可能是继续论述共轭直径。^[4]阿波罗尼奥斯处理圆锥曲线的方法与前人不同，不用三个圆锥，只用一个圆锥，通过改变截面的位置产生三种曲线，他还注意到截面垂直于轴时截线是圆。他最先发现双曲线是有心曲线，并有两个分支，他对圆锥曲线的叙述很接近近代方式。例如，（以顶点为原点，轴为横轴的抛物线）任一点横坐标与通径组成的矩形等于与之对应的纵坐标组成的正方形；（以一顶点为原点，长轴为横轴的椭圆或双曲线）任一点纵坐标组成的正方形小于或大于与之对应的横坐标及通径组成的矩形。表示为现代形式，即y2=px，y2＜px，y2＞px。根据他的表述，圆锥曲线方程可以表达为y2=px（抛物线），y2=px-（椭圆），或y2=px+（双曲线）（其中p 为通径，d 为与之对应的直径）。

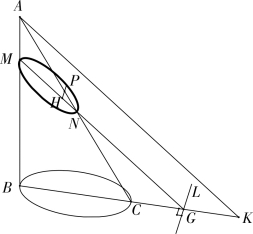
图1-1-2

以椭圆的定义为例。如图1-1-2，A-BC是一圆锥面（不一定为正圆锥面），设锥的一截面与底平面的交线为GL，GL 在底圆之外，与圆锥面的交线曲线为MPN。在底面取垂直于GL 的直径BC，并延长交GL 于G 点。轴平面与曲线MPN 交于M 和N。轴平面内过A 作AK∥MG 交BG 的延长线于K 点。MPN 便是轴平面ABC 与截平面的交线。在截曲线上任取一点P，作PH∥GL 交MN 于H 点。阿波罗尼奥斯称PH 为纵标线，他希望对曲线上任一点建立起纵标线PH 与同样依赖P 点位置的线段MH 之间的关系。

阿波罗尼奥斯作了一系列的辅助线和几何推理得到

对于给定的圆锥面与截平面，MN，BK，CK 均为确定的线段，若记

这样阿波罗尼奥斯相当于给出解析几何中的椭圆方程

由于y2=px，y2＜px，y2＞px，便称抛物线、椭圆、双曲线分别为“齐曲线”“亏曲线”“盈曲线”。当希腊著作传入欧洲时，这些名称便译为拉丁文之“Parabola”“Ellipse”“Hyperbola”。

阿波罗尼奥斯用统一的方式引出圆锥三曲线后，对它们的性质进行广泛的讨论，内容涉及圆锥曲线的直径，共轭直径、切线、中心、双曲线的渐近线、椭圆与双曲线的焦点以及处在各种不同位置的圆锥曲线的交点数等等。

《圆锥曲线论》用纯欧氏几何的方法得到了现在解析几何的几乎全部的主要结论，令人叹服。该书被认为代表了希腊演绎几何的最高成就，是圆锥曲线论创立的标志性著作。

阿波罗尼奥斯以后，希腊对圆锥曲线的贡献显得不多。4世纪，由于帕普斯的研究，希腊几何又兴盛起来。帕普斯是当时著名的几何学家，很多著作都失传了，只流传下来他的《数学论丛》后6 卷（这书共8 卷，前2 卷已散佚）。由《数学论丛》可以看出他对圆锥曲线有很多贡献，例如卷8 证明了五点可确定一条圆锥曲线，卷7 证明了圆锥曲线的焦点-准线-离心率性质，等等。