例19-1 质量为m=0.5kg的物块，沿光滑斜面无初速滑下，如图19-11所示。当物块下落高度h=0.1m时撞于无质量的弹簧上并与弹簧不再分离。弹簧刚度系数k=0.8kN/m，斜面倾角β=30°，求此系统振动的固有角频率和振幅，并给出物块的运动方程。
已知：m=0.5kg，h=0.1m，k=0.8kN/m，β=30°。
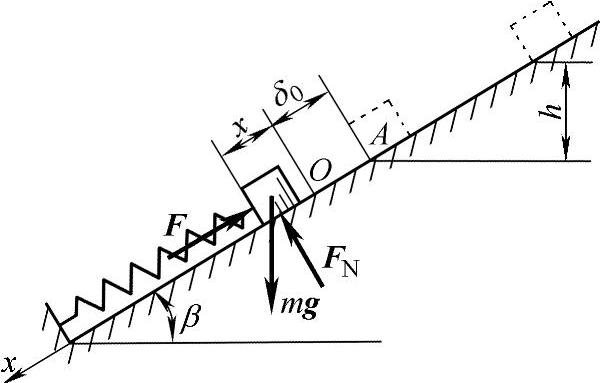
图19-11 例19-1图
求：ω0，A，x=x（t）。
解：●建模
物块受力：mg，FN，F。物块作直线运动。
●Maple程序
答：此系统振动的固有角频率ω0=40rad/s和振幅A=35.13mm，物块的运动方程x=35.13sin（40t-0.08724）mm（式中t以s计）。
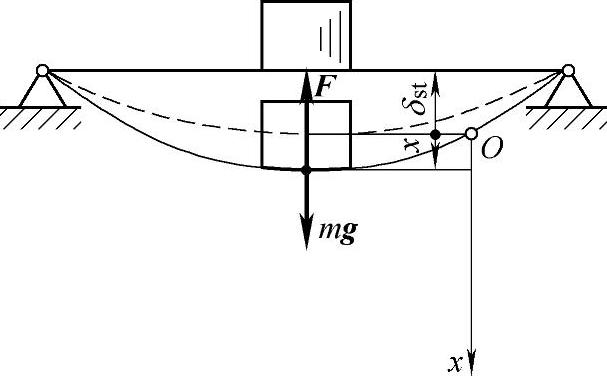
图19-12 例19-2图
例19-2 图19-12所示为一无重弹性梁，当其中部放置质量为m的物块时，其静挠度为2mm。若将此物块在梁未变形位置处无初速度释放，求系统的振动规律。
已知：m，δst=2mm，v0=0。
求：x=x（t）。
解：●建模
物块受力：mg，F。物块作直线运动。
●Maple程序
答：系统的振动规律x=-2cos（70t）mm（式中t以s计）。
例19-3 图19-13所示为一摆振系统，杆重不计，球质量为m，摆对轴O的转动惯量为J。弹簧刚度系数为k，杆处于水平位置平衡，尺寸如图所示。求此系统微小振动的运动微分方程及振动频率。
已知：m，J，k，l，d。
求：ω0，系统微小振动的运动微分方程。
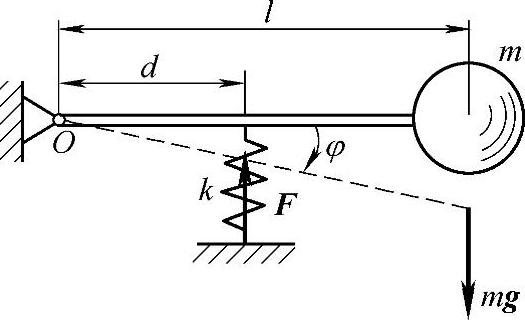
图19-13 例19-3图
解：●建模
摆受力：FOx，FOy，mg，F。摆作定轴转动。
●Maple程序
答：系统微小振动的运动微分方程为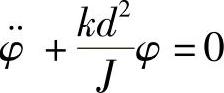
；振动频率
。
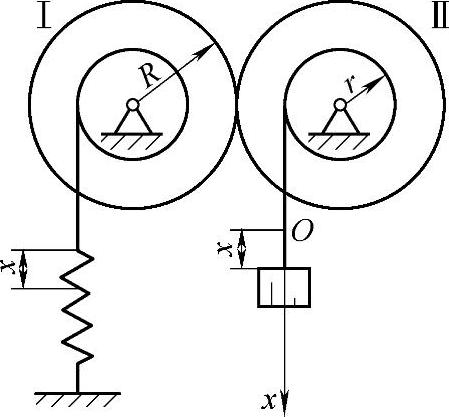
图19-14 例19-4图
例19-4 图19-14所示两个相同的齿轮，相啮合的齿轮半径皆为R；半径为r的鼓轮上绕有细绳，轮Ⅰ连一铅垂放置的弹簧，轮Ⅱ挂一重物。齿轮对轴的转动惯量皆为J，弹簧刚度系数为k，重物质量为m。求此系统振动的固有角频率。
已知：m，J，k，R，r。
求：ω0。
解：●建模
采用拉格朗日方程。系统受主动力：mg，Fk。轮Ⅰ作定轴转动；轮Ⅱ作定轴转动；重物作直线运动。以系统平衡位置时重物的位置为原点，取x轴如图所示。系统有一个自由度。从平衡位置起计算弹性势能时，不再计入重力，弹簧的变形量按x计算，而不是x+δst。
●Maple程序
答：系统振动的固有角频率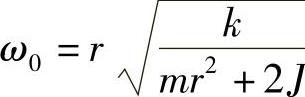
J。
例19-5 在图19-15所示振动系统中，摆杆OA对铰链点O的转动惯量为J，在杆的点A和B各安置一个弹簧刚度系数分别为k1和k2的弹簧。系统在水平位置处于平衡，求系统作微振动时的固有角频率。
已知：J，k1，k2，l，d。
求：ω0。
解：●建模
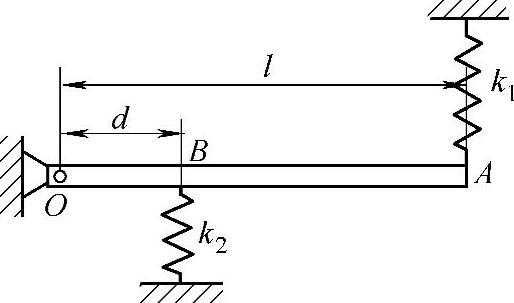
图19-15 例19-5图
采用能量法。系统受主动力：mg，Fk1，Fk2。摆作定轴转动。摆杆的最大角位移为Φ，若选择平衡位置为零势能点，计算势能时可以不管重力，而由平衡位置计算弹性变形。
●Maple程序
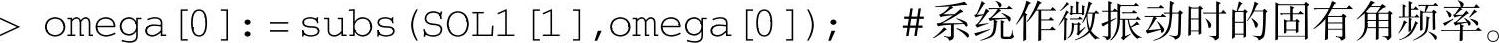
答：系统作微振动时的固有角频率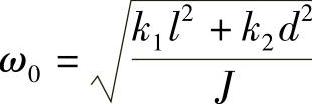
。
例19-6 图19-16表示一质量为m、半径为r的圆柱体，在一半径为R的圆弧上作无滑动的滚动。求圆柱体在平衡位置附近作微小振动的固有角频率。
已知：m，r，R。
求：ω0。
解：●建模
采用能量法。系统受主动力：mg。圆柱体作平面运动。系统的势能即为重力势能，圆柱在最底处处于平衡状态，取该处圆心位置C为零势能点。
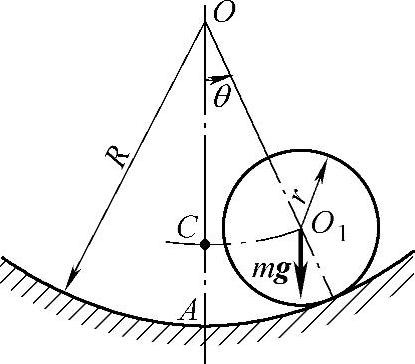
图19-16 例19-6图
●Maple程序
答：圆柱体在平衡位置附近作微小振动的固有角频率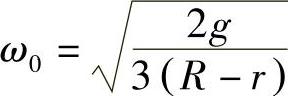
。
例19-7 图19-17所示为一弹性杆支持的圆盘，弹性杆扭转刚度系数为kt，圆盘对杆轴的转动惯量为J。如果圆盘外缘受到与转动速度成正比的切向阻力，而圆盘衰减扭振的周期为Td。求圆盘所受阻力偶矩与转动角速度的关系。
已知：kt，J，Td。
求：μ。
解：●建模
系统受主动力：Mn，Mz。圆盘作定轴转动。
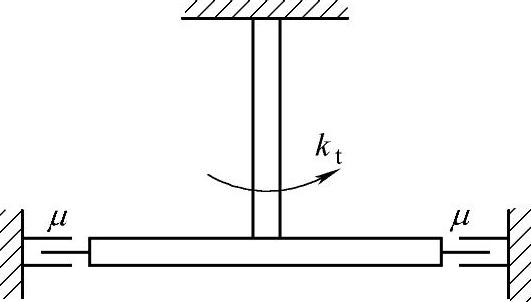
图19-17 例19-7图
●Maple程序
答：圆盘所受阻力偶矩Mz与转动角速度ω成正比，阻力偶系数
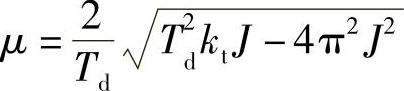
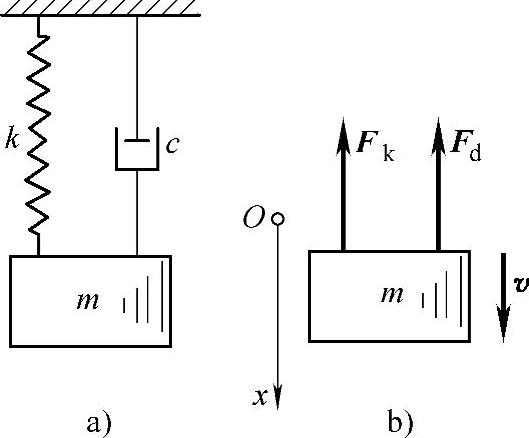
图19-18 例19-8图
例19-8 如图19-18所示质量-弹簧阻尼系统，其物块质量为0.05kg，弹簧刚度系数k=2kN/m。使系统发生自由振动，测得其相邻两个振幅之比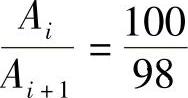
。求系统的临界阻尼系数和阻尼系数各为多少？已知：m=0.05kg，k=2kN/m，
。
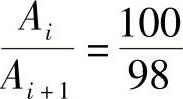求：ccr，c。
解：●建模系统受主动力：mg，Fk，Fd。物块作直线运动。
●Maple程序
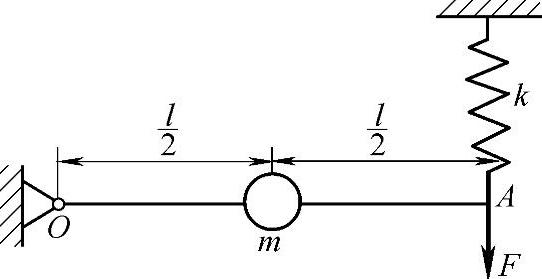
图19-19 例19-9图
答：系统的临界阻尼系数ccr=20N·s/m和阻尼系数c=0.06302N·s/m。
例19-9 图19-19所示为一长为l无重刚杆OA，其一端O铰支，另一端A水平悬挂在刚度系数为k的弹簧上，杆的中点装有一质量为m的小球。若在点A加一激振力F=F0sinωt，其中激振力的频率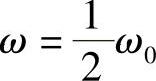
，ω0为系统的固有角频率。忽略阻尼，求系统的受迫振动规律。
已知：l，k，m，F=F0sinωt，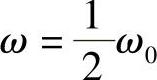
。
解：●建模(www.daowen.com)
系统受主动力：mg，Fk，F。摆作定轴转动。
●Maple程序
答：系统的受迫振动规律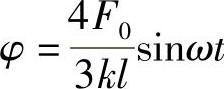
。
例19-10 图19-20表示带有偏心块的电动机固定在一根弹性梁上，设电动机的质量为m1，偏心块的质量为m2，偏心距为e，弹性梁的刚度系数为k，求当电动机转子以匀角速度ω旋转时系统的受迫振动规律。
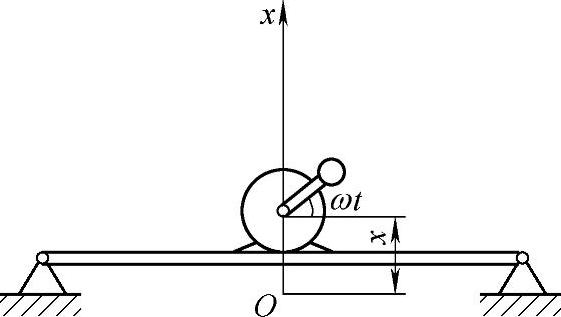
图 19-20 例19-10图
已知：m1，m2，e，k，ω。
求：x=x（t）。
解：●建模
采用动量定理。电动机与偏心块组成的系统受主动力：m1g，m2g，Fk。偏心块作圆周运动。
●Maple程序
答：当电动机转子以匀角速度ω旋转时系统的受迫振动规律x=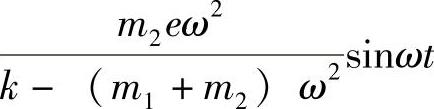
。
例19-11 图19-21所示为一测振仪的简图，其中物块质量为m，弹簧刚度系数为k，测振仪放在振动物体表面，将随物体而运动，设被测物体的振动规律为s=esinωt，求测振仪中物块的运动微分方程及其受迫振动规律。
已知：m，k，s=esinωt。
求：x=x（t）。
解：●建模
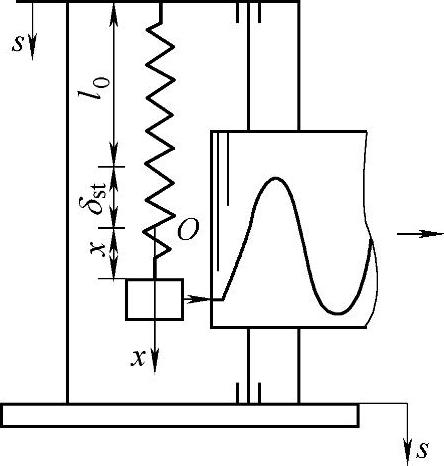
图19-21 例19-11图
物块受主动力：mg，F。物块作直线运动。
●Maple程序
答：测振仪中物块的运动微分方程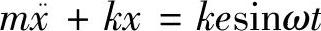
，受迫振动规律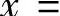
。
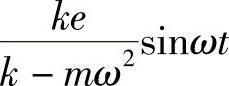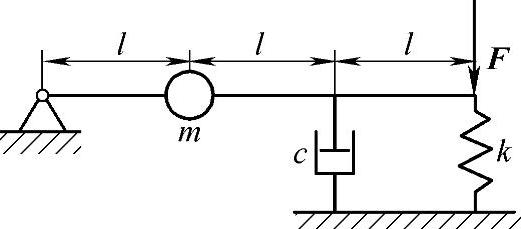
图19-22 例19-12图
例19-12 图19-22所示为一无重刚杆。其一端铰支，距铰支端l处有一质量为m的质点，距2l处有一阻尼器，其阻尼系数为c，距3l处有一刚度系数为k的弹簧，并作用一简谐激振力F=F0sinωt，刚杆在水平位置平衡，试列出系统的振动微分方程，并求系统的固有角频率ω0，以及当激振力角频率ω等于ω0时质点的振幅。
已知：m，l，2l，3l，c，k，F=F0sinωt。
求：ω0，B。
解：●建模
物块受主动力：mg，Fk，Fd，F。刚杆作定轴转动。
●Maple程序
答：系统的振动微分方程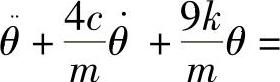
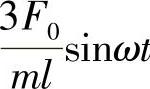，系统的固有角频率
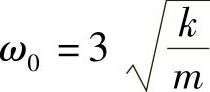，以及当激振力角频率ω=ω0时质点的振幅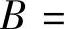
。
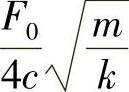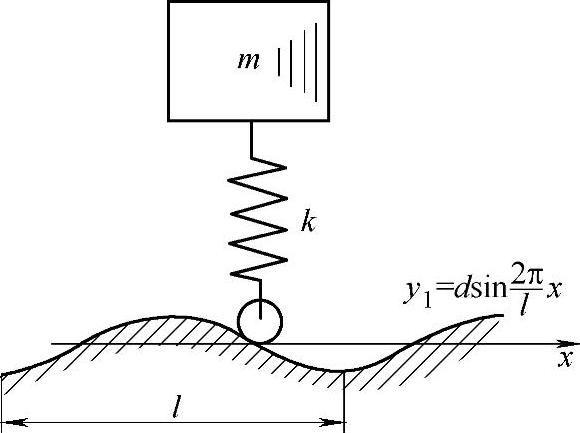
图19-23 例19-13图
例19-13 图19-23所示为一汽车在波形路面行走的力学模型。路面的波形可以用公式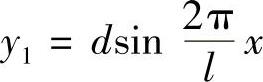
表示，其中幅度d=25mm，波长l=5m。汽车的质量为m=3000kg，弹簧刚度系数为k=294kN/m。忽略阻尼，求汽车以速度v=45km/h匀速前进时，车体的垂直振幅为多少？汽车的临界速度为多少？
已知：m=3000kg，d=25mm，l=5m，ζ=0，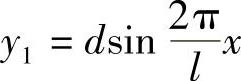
，v=45km/h，k=294kN/m。
求：b，vcr。
解：●建模
汽车受主动力：mg，Fk。汽车作曲线运动。汽车运动微分方程：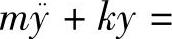
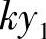。本题相当于被动隔振问题。
●Maple程序
答：车体的垂直振幅为b=16.47mm。汽车的临界速度为vcr=28.36km/h。
例19-14 用Maple进行单自由度系统的机械振动计算分析。
本题试图从Maple编程角度出发，对单自由度振动系统特性进行分析，产生极好的仿真，并以期为实际工作提供一定的借鉴，当然运用MATLAB/SIMULINK仿真工具可进行一些系统仿真，但编程更能发挥人们的想象力和创造力，能方便地解决工程上多变的实际问题。
由振动理论可知，在不同阻尼条件下，受迫振动的幅频特性是不同的，且阻尼对振幅的影响与频率有关，下面将探讨用Maple仿真在相同阻尼下不同激振力频率Ω的有阻尼受迫振动，这里取阻尼比ζ=0.2，ω0=1，h=1，x0=0，v0=1。
已知：ζ=0.2，ω0=1，h=1，x0=0，v0=1。①Ω=0.02；②Ω=0.999；③Ω=5。
求：（1）x=x（t）。（2）绘幅频特性曲线、相频特性曲线和幅-频-阻尼曲面。
解：（1）●建模
单自由度阻尼受迫振动方程为
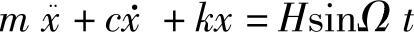
化成
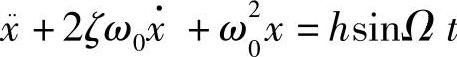
得
x=Ae-ζω0tsin（ωdt+α）+Bsin（Ωt-θ）
其中参数：固有角频率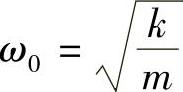
，阻尼比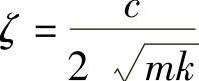
，有阻尼自由振动角频率
，
，
，
，
，
。
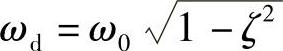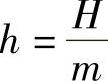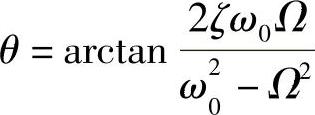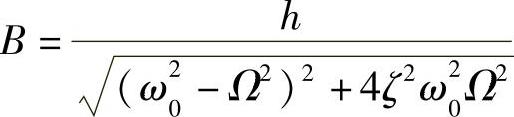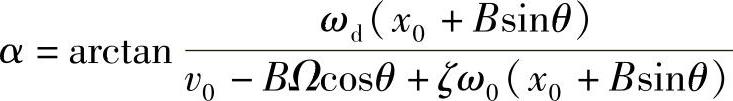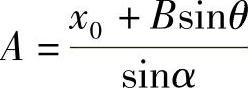●Maple程序
1）当Ω=0.02（<<ω0）时，振动方程为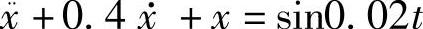
，计算结果为
x=1.002e-0.2tsin（0.9798t+0.07989）+sin（0.02t-0.008004）该结果由两部分组成，第一部分是衰减自由振动，第二部分是受迫振动、稳态解。用Maple编程可求得上述结果并可仿真输出振动波形。
执行此程序即可得计算结果与图19-24所示的振动曲线。该波形直接反映了整个受迫振动的过程，由振动方程的解和振动曲线均可见振幅B=1，相位θ=0.008。显然用Maple编程能较方便地解出振动方程的解，并快速地输出振动曲线。当振动方程参数不同时，只需在Maple程序中改变相应变量初始化值即可。下面给出的是Ω取另外两个值时的情况。
2）当Ω=0.999（≈ω0）时，振动方程为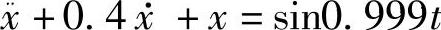
，计算结果为
x=2.927e-0.2tsin（0.9798t+1.025）+2.502sin（0.999t-1.566）在Maple程序中需改变Ω初始化值，先令Ω=0.999再运行该程序，输出波形如图19-25所示，可见这时振幅较大，B≈2.5，相位θ=1.566接近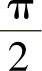
。
3）当Ω=5（>>ω0）时，振动方程为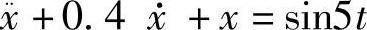
，计算结果为
x=1.233e-0.2tsin（0.9798t+0.002813）+0.04153sin（5t-3.058）在Maple程序中需改变Ω初始化值，先令Ω=5再运行该程序，输出波形如图19-26所示，可见这时振幅B≈0.04，相位θ=3.058接近π，激振力与位移反向。
由上述这些试验结果可见，单自由度阻尼系统振动输出由衰减项和稳定项两部分组成，当激振角频率Ω取不同值时，阻尼对振幅B和相位θ的影响是不同的。从这些Maple输出的振动曲线显然可见，在阻尼比ζ相同情况下的幅频特性，当激振角频率接近系统的固有角频率ω0时，振幅明显增大，从图19-24～图19-26中均可见有阻尼受迫振动整个过渡阶段的衰减和稳态过程。以上方法可适用于各种初始条件下阻尼振动给出精确的解析解和几何描述。
（2）●建模
对受迫振动在不同阻尼条件下的幅频关系曲线进行仿真，较方便地对振动方程求解，并画出相应的振动波形，精确地分析系统固有振动特性。由式（19-24）可知，振幅比和相位分别为
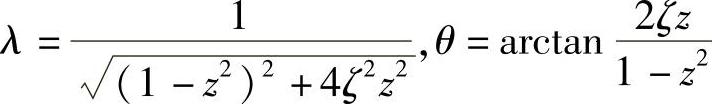
图19-27所示为幅频关系曲线；图19-28所示为相频关系曲线；并可输出图19-29所示的三维幅-频-阻尼曲面。
●Maple程序
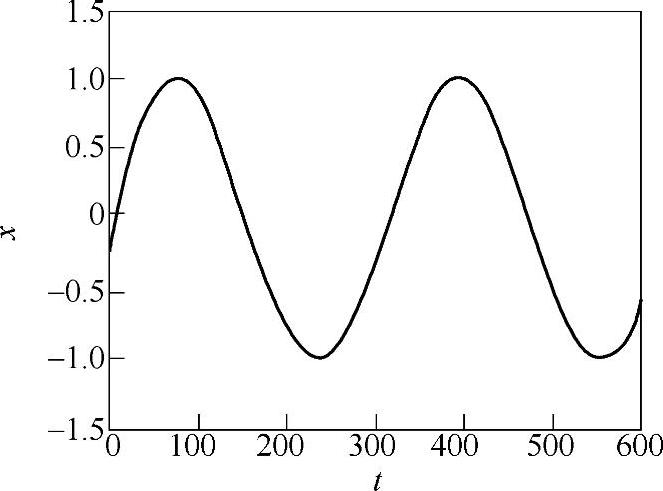
图19-24 低频激励时程曲线
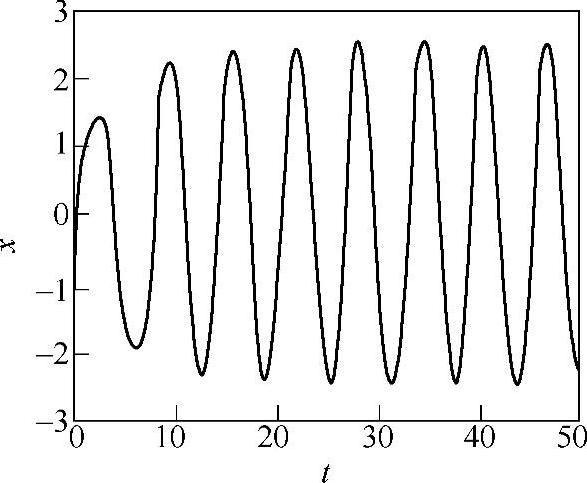
图19-25 共振时程曲线
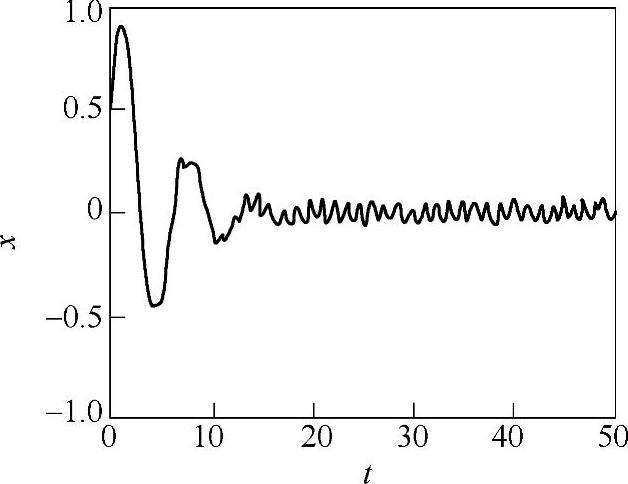
图19-26 高频激励时程曲线
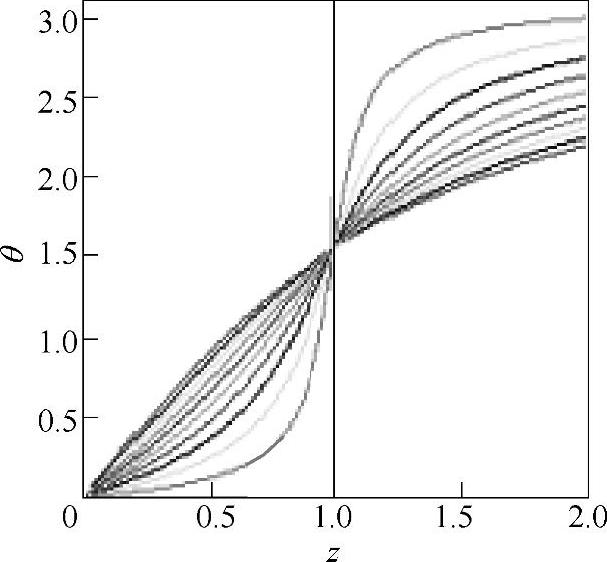
图19-28 相频曲线
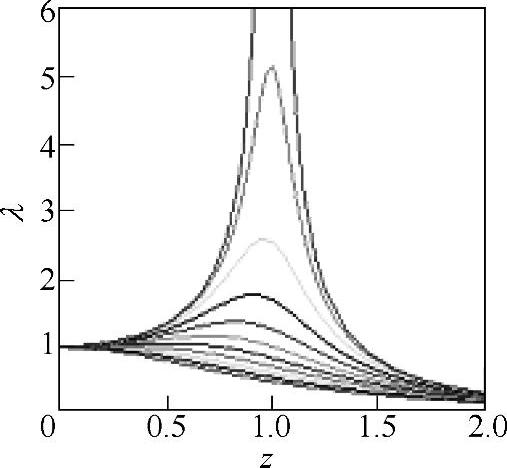
图19-27 幅频曲线
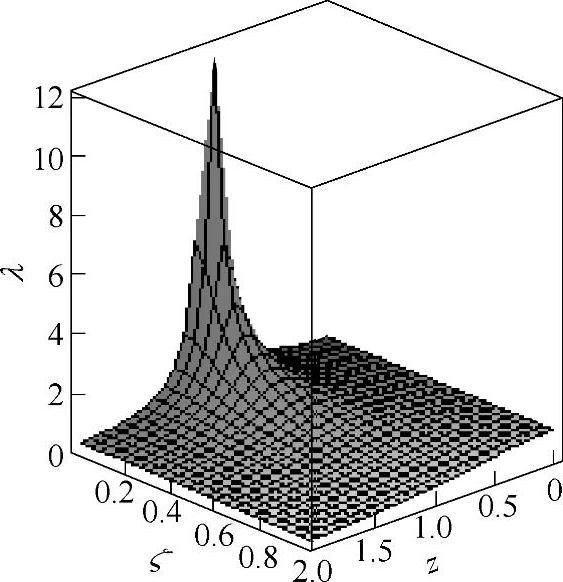
图19-29 三维幅-频-阻尼曲面
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
