设质点除受弹性回复力、线性阻尼力作用外，还有外界激励力。现只研究激励力为简谐变化的情况（图19-6）。即

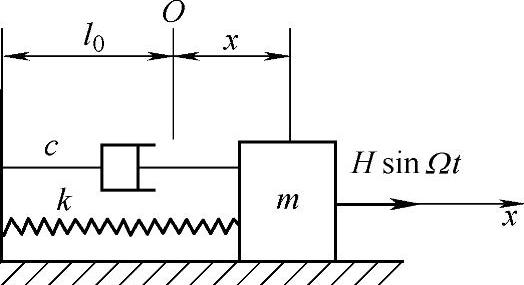
图19-6 受激励的质量弹簧系统

F=HsinΩt （a）则质点的运动微分方程为

或化为标准形式为

式中，

式（19-18）为线性非齐次微分方程，其解由两部分组成，即

x（t）=x₁（t）+x₂（t） （19-19）

式中， x₁（t）=Ae^-δtsin（ω_dt+α） （19-20）

x₂（t）=Bsin（Ωt-θ） （19-21）

其中x=x₁（t）为齐次部分的通解，x=x₂（t）为非齐次方程的特解；将式（19-21）代入方程式（19-18），可解出B与θ。其表达式为

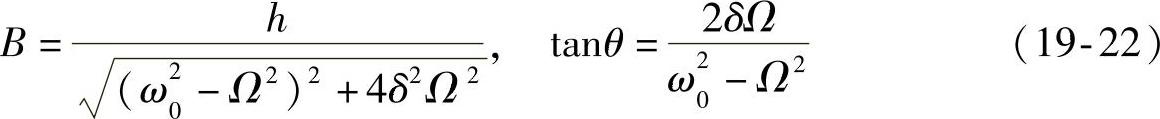
在简谐激励力作用下，质点位移的时间历程如图19-7所示。由图可清楚看出，时间历程有过渡过程及稳态过程两个阶段；稳态过程又称系统对激励力的稳态响应，它是一个由x₂（t）代表的稳定的振动，且只与系统及激励力的参数有关，与运动初始条件无关；过渡过程又称系统对激励力的瞬态响应，它是衰减振动与稳态振动的叠加，且与初始条件有关。一般情况下，过渡过程很快结束，所以我们有兴趣的主要是稳态过程，除非特别指明研究瞬态响应。

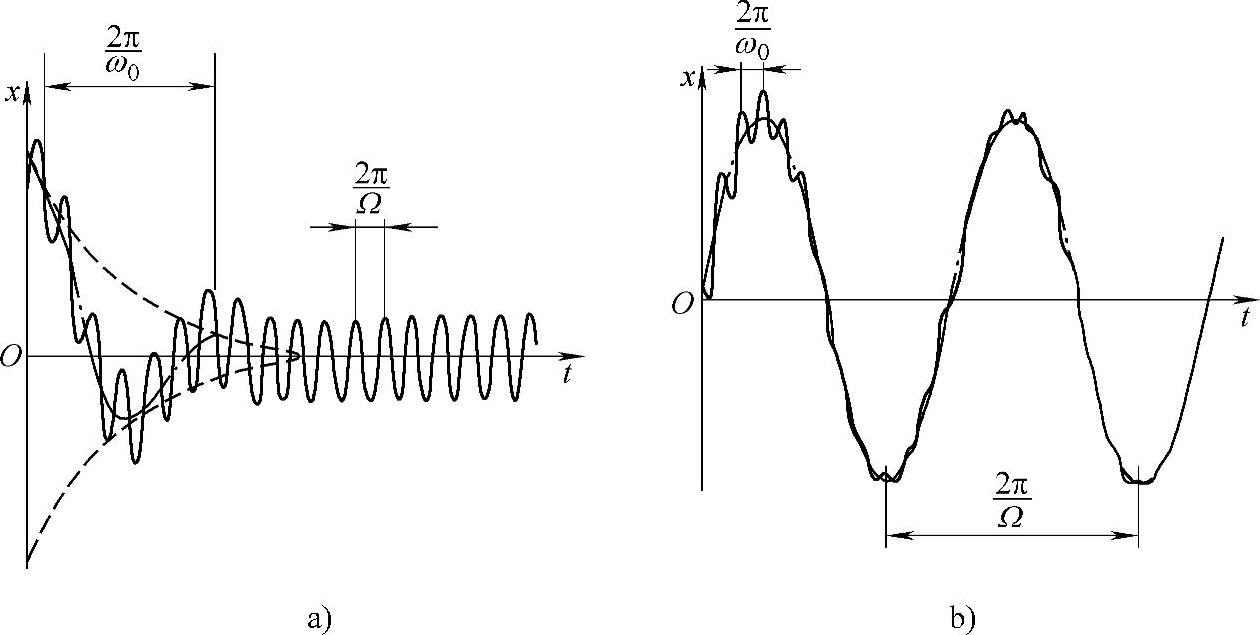
图19-7 瞬态响应与稳态响应

a）Ω>ω₀ b）Ω<ω0

相对自由振动、衰减振动而言，x=x₂（t）所代表的稳态过程又称受迫振动。为研究受迫振动的特性，首先使式（19-22）量纲为一。引入量纲为一的参数λ，z，ζ，则(www.daowen.com)

式中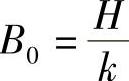，，表示在常力H作用下弹簧的位移，称为质点的静力偏移；λ是在幅值为H的激励力作用下质点的振幅与静力偏移之比，称为放大因子；z是激励力角频率与固有角频率之比，称为角频率比；ζ是已经用过的阻尼比。这时确定质点受迫振动的振幅及相位差的式（19-22）可量纲为一化为

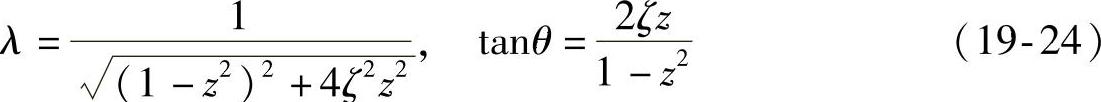
上式可用图形表示，曲线λ-z称为幅频特性曲线，θ-z称为相频特性曲线（图19-8a、b）。

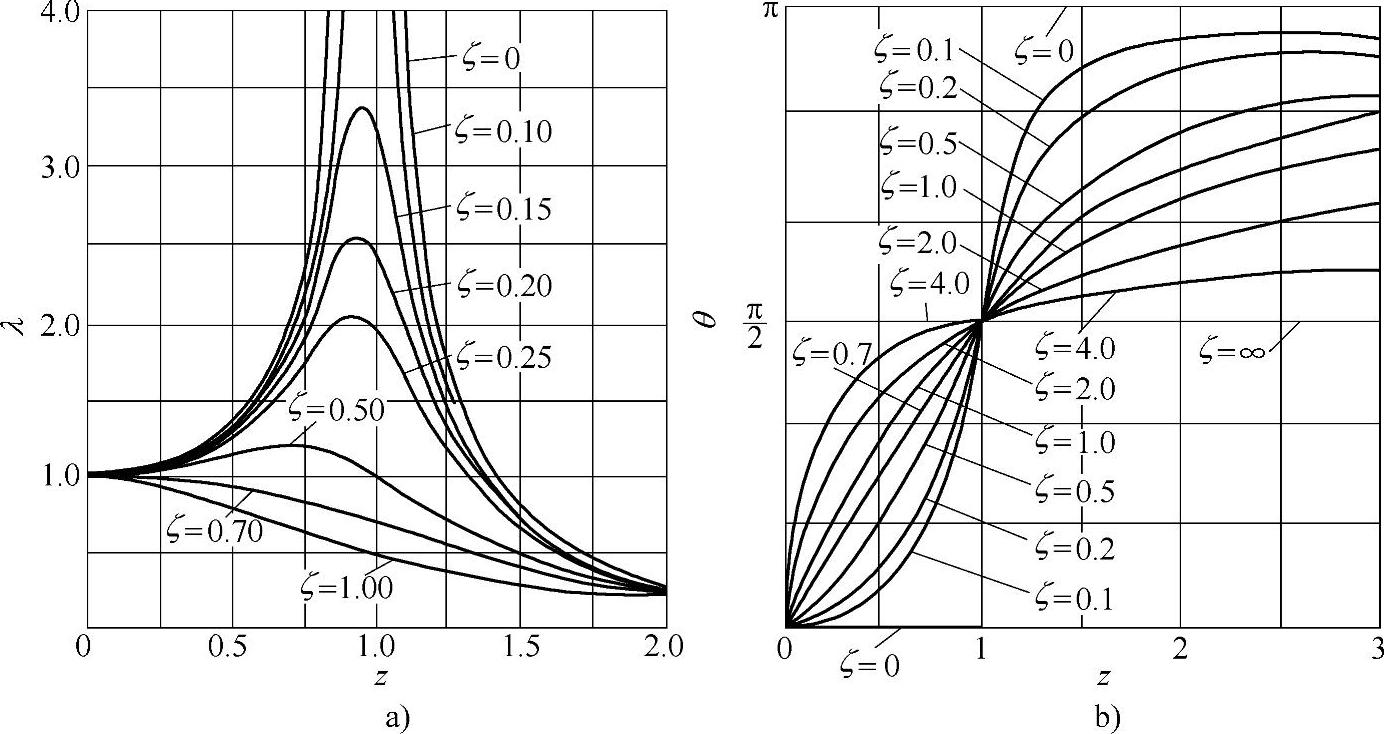
图19-8 幅频特性曲线与相频特性曲线

由式（19-24）及图19-8可以归纳出受迫振动的一些特性如下：

1）受迫振动是振幅恒定的振动，其频率与激励力的频率相同，但有相位差。受迫振动的振幅与相位差只取决于系统及激励力的参数，与运动的初始条件无关。

2）当激励力的频率与系统的固有频率接近时，受迫振动的振幅急剧增加，这种现象称为共振；因此，幅频特性曲线又称共振曲线。对无阻尼受迫振动，共振频率准确等于固有频率；阻尼很小时，共振频率略低于固有频率。在共振区，阻尼的增加可以显著降低共振振幅。

3）在幅频特性曲线上，除共振区（z≈1）外，还有低频区（z<<1）及高频区（z>>1）。在低频区，激励力的频率远小于固有频率，即振动系统受到“低频”的外部扰动；这时受迫振动振幅接近静力偏移。在高频区，激励力的频率远大于固有频率，即振动系统受到“高频”的外力扰动；这时受迫振动振幅几乎趋近于零，其物理意义是：在高频扰动下，质点来不及振动，因而振幅很小。

4）在相频特性曲线上可以看到，在小阻尼ζ<<1情况下，对z<<1有θ≈0，对z>>1有θ≈π；亦即在低频激励时，受迫振动与激励力同相，而在高频激励时，受迫振动与激励力反相。当z=1，即共振时，不管阻尼如何，相位差总为θ=π/2。

上述结论能通过一个简单的表演观察到（图19-9）。弹性绳的一端连接一重物，另一端用手提起处于铅垂位置；先给弹性绳一初始伸长，根据衰减振动估计出系统的固有频率。再将持绳的手上下振动，这相当于在重物上作用了一个周期性的激励力，观察重物的受迫振动。当手的振动是低频时，重物作与手的振动接近的同频受迫振动，而且是同相；当手的振动是高频时，重物作同频的反相振动，且振幅很小；当手的振动频率很高时，重物几乎不动；当手的振动频率与固有频率接近时，重物的振幅不断加大，出现共振现象。

共振现象在工程上十分重要。共振的巨大振幅足以使结构疲劳甚至破坏，在实际工程中多数情况下应该避免，大家都知道排队的士兵过桥时只能便步走，就是为了避免齐步走时步伐的激励造成桥梁铅垂方向的共振，特别是对一些固有频率较低且接近步伐频率的吊桥及悬索桥。旋转机械的转子如果不平衡，则旋转时不平衡量的离心惯性力在铅垂方向与水平方向的投影都是周期性的激励力，如果转子的转速与转子系统（转子及支承组成的系统）横向振动固有频率相等或接近时，转子系统将发生横向共振，这时的转速称为转子的临界转速。设计旋转机械时，必须使转子的工作转速远离临界转速，这可以通过改变转子系统的结构参数（如m，k等）达到。在非共振情况下也需控制受迫振动的振幅，利用共振曲线（图19-8a）及式（19-24）进行设计。

一些精密仪器不能直接安装在楼板上，因为楼板的振动会影响仪器的正常工作。这时可以在仪器与楼板之间设置弹簧，如图19-10所示，当楼板上下振动时，仪器就作受迫振动。根据图19-8中的幅频特性曲线可知，当z>>1时受迫振动的振幅接近于零。因此，应该用软的弹簧，使仪器与弹簧系统的固有频率大大低于楼板的振动频率，亦即形成高频干扰；这时仪器的振幅可以很小，因而能正常工作。实际工程中多采用减震垫，它既有弹性又有阻尼（与相对速度成比例），这时仪器的受迫振动运动特性与图19-8不同，有兴趣的读者可参考有关隔振理论的书籍。

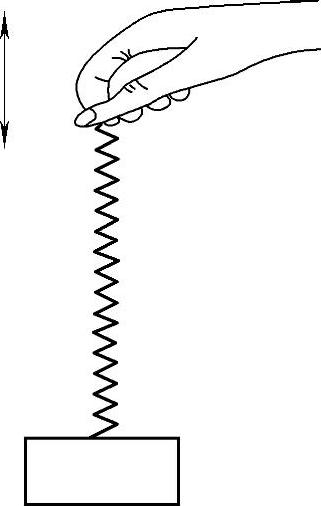
图19-9 受迫振动表演

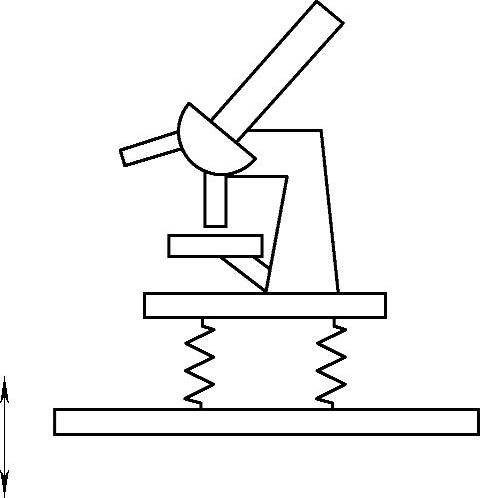
图19-10 仪器的隔振