有阻尼质量-弹簧系统如图19-4所示，设阻力与速度成比例，c称为阻尼系数。即

那么运动微分方程（19-4）改变成为

或写成

其中常量

式中，ζ称为阻尼比，微分方程（19-12）的特征方程是

λ²+2δλ+ω₀²=0 （c）

特征根为

式中，i为虚数单位，并设δ<ω₀，即ζ<1。微分方程（19-12）的通解为

x=Ae^-δtsin（ω_dt+α） （19-15）(www.daowen.com)

式中，δ，ω_d取决于系统参数，而A，α取决于运动初始条件。式（19-15）所表示的x的时间历程曲线如图19-5所示。由于振幅不断衰减，故有阻尼的自由振动是衰减振动，由图可以总结出衰减振动的运动特性如下：

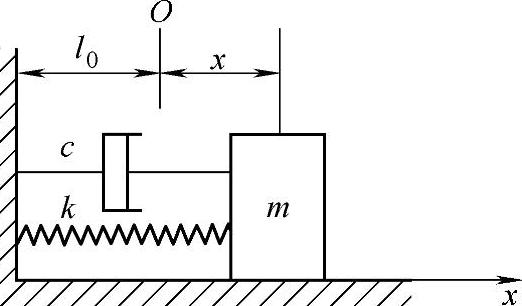
图19-4 有阻尼质量-弹簧系统

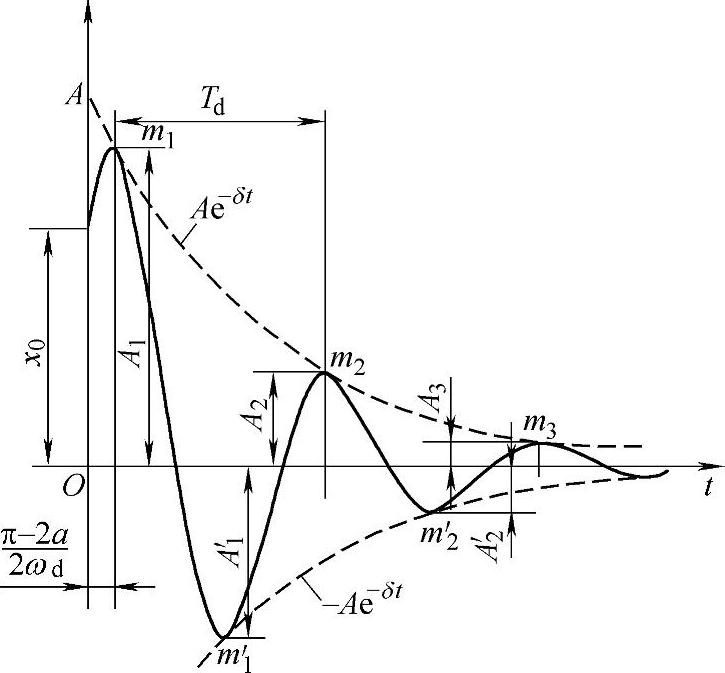
图19-5 衰减振动的时间历程

1）严格地讲，在小阻尼ζ<1的情况下，运动不再是周期的。但由于式（19-15）中含sin（ω_dt+α）的因子，故仍可定义衰减振动的频率ω_d及衰减振动的周期T_d=2π/ω_d，且知其频率小于无阻尼自由振动频率，即ω_d<ω₀。

2）振幅按几何级数衰减，每经过一个周期T_d，振幅的衰减率均相同，有

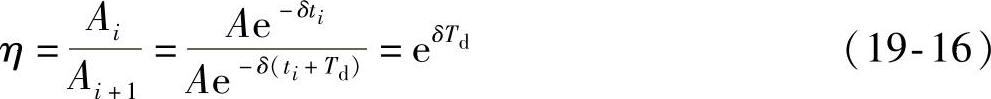
式中，η称为减幅系数，有时用其对数Λ=δT_d表示，称为对数减缩。如果阻尼比为ζ=0.05，则可算出：

可以看出，衰减振动的频率只与自由振动的频率相差0.5%，但每经过一个周期，振幅要衰减27%；亦即小阻尼对振动的频率与周期影响很小，甚至可以忽略，但对振幅衰减的作用却十分显著。

3）对大阻尼ζ>1及临界阻尼ζ=1，由特征根式（19-14）的分析可知，衰减运动不再有往复性质。