在稳定平衡位置附近运动是力学系统的一种非常普遍的运动类型,称为微振动。我们从最简单的情况开始研究这种运动,即系统只有一个自由度。
稳定平衡位置是指势能取极小值的位置,偏离该位置会导致产生力-dV/dq,从而使系统返回平衡位置。我们用q0表示其相应的广义坐标值。在偏离平衡位置很小的情况下,在V(q)-V(q0)按q-q0展开的表达式中保留第一个非零项就足够了。一般情况下这是二阶项,即

式中,k为正数(是二阶导数V″(q)在q=q0处的值)。今后我们从势能的最小值开始计算势能(即假设V(q0)=0),并引入记号
x=q-q0 (19-1)
表示偏离平衡位置的坐标。于是有

单自由度系统的动能一般可以写成为

同样地,近似函数a(q)可以用它在q=q0处的值代替。引入记号(需要强调的是,只有当x是笛卡儿坐标时m才是质量)
a(q0)=m (19-3)
最后可得一维振动系统的拉格朗日函数表达式如下:

相应的运动方程为

或者

这里引入了记号

线性微分方程(19-5)的两个线性无关的解为cosω0t和sinω0t,因此方程的通解为
x=c1cosω0t+c2sinω0t (d)
这个表达式可以写成为
x=asin(ω0t+α) (19-7)
因为x=asin(ω0t+α)=asinω0tcosα+acosω0tsinα,与式(d)比较可得任意常数a和α与常数c1和c2的关系:

于是,系统在稳定平衡位置附近的运动是简谐运动。式(19-7)中周期因子前面的系数a称为振幅,而余弦辐角称为振动的相位,α是相位的初始值,称为初相位,显然它依赖于初始时间的选择。物理量ω0是振动的基本特征量,不依赖于运动的初始条件。根据式(19-6),它完全由力学系统本身的性质决定,称为系统的固有角频率。但是应该指出,这个特点与小幅振动假设相关,对于大幅振动不成立。从数学角度看,通常它与势能是坐标的二次函数有关。
微振动系统的能量为

或者,将式(19-7)代入此式得

这与振幅的平方成正比。
振动系统坐标对时间的依赖关系经常写成复数表达式的实部形式:
x=Re(Aeiω0t) (19-10)
式中,A是复常数,写成下面形式:
A=aeiα (19-11)
这样我们又回到式(19-7)了。常数A称为复振幅,它的模就是通常的振幅,而辐角就是初始相位。(https://www.daowen.com)
在数学上,指数函数运算比三角函数运算简单,因为指数函数的微分不改变形式。当我们进行线性运算时(加法、数乘、微分和积分),一般可以不写出取实部的记号,只需对最后的计算结果取实部。
习题1 试用坐标和速度的初始值x(0)=x0和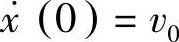 表示振幅和初始相位。
表示振幅和初始相位。
答:
习题2 工程中常遇到质点在铅垂方向的振动,这时质点还受重力作用。
解:参照图19-1a,质点的运动微分方程为

其解为
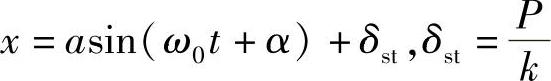
亦即质点仍作频率为ω0的简谐振动,只是振动中心位于x=δst处,δst为弹簧的静伸长。由此可知:常力只改变振动中心的位置。引入静伸长δst,还可将固有角频率及周期改写为
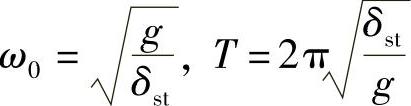
如果将参考坐标的原点取在弹簧静伸长处,如图19-1b所示,则运动微分方程改变,但解的形式简单。其表达式为
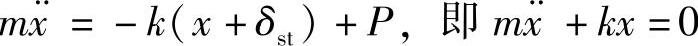
x=asin(ω0t+α)

图19-1 常力对质量-弹簧系统的作用
习题3 设质量为m的质点沿着直线运动,弹簧一端连在质点上,另一端固定于A点(图19-2)。A点到直线的距离为l,弹簧长度为l时受力为F,试求微振动角频率。
解:弹簧势能等于力F乘以弹簧伸长量δl(精确到更高阶小量)。当x<<l时,有
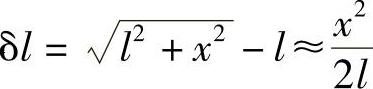
因此,V=Fx2/(2l)。因为动能为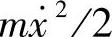 ,故
,故
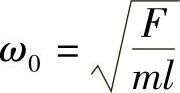
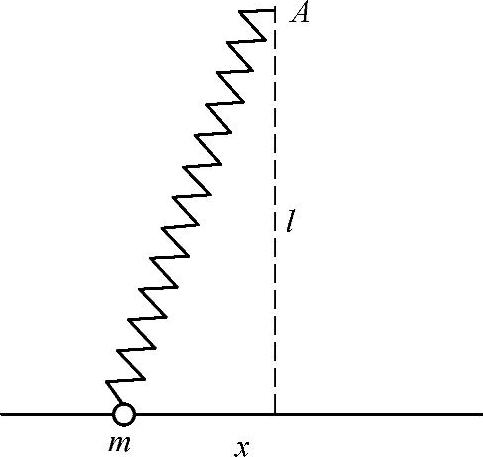
图 19-2
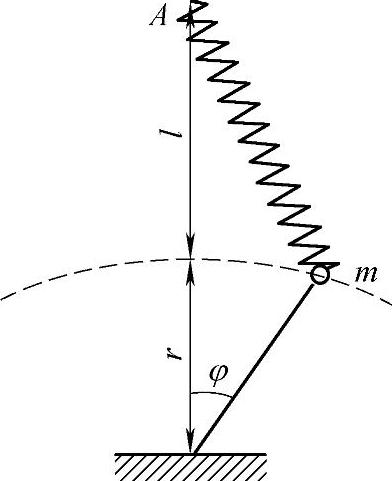
图 19-3
习题4 同上题,质量为m的质点沿着半径为r的圆运动(图19-3)。
解:在这种情况下,弹簧伸长量为(在φ<<1时)
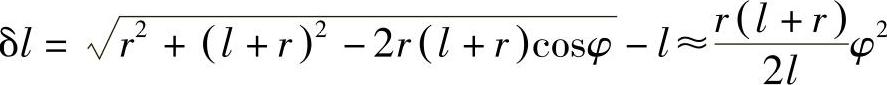
动能为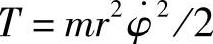 。由此得角频率
。由此得角频率
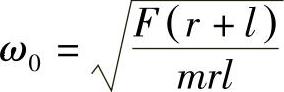
习题5 试求图18-2的平面摆的角频率,悬挂点质量为m1,并且可沿着水平方向运动。
解:当φ<<1时,有
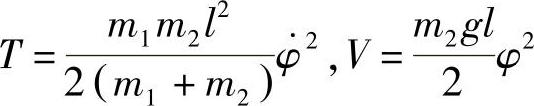
由此得
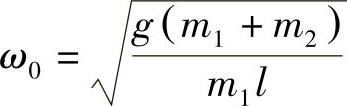
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






