例18-1 杆OA和AB以铰链相连,O端悬挂于圆柱铰链上,如图18-8所示。杆长OA=a,AB=b,杆重和铰链的摩擦都忽略不计。今在点A和B分别作用向下的铅垂力FA和FB,又在点B作用一水平力F。试求平衡时φ1,φ2与FA,FB,F之间的关系。
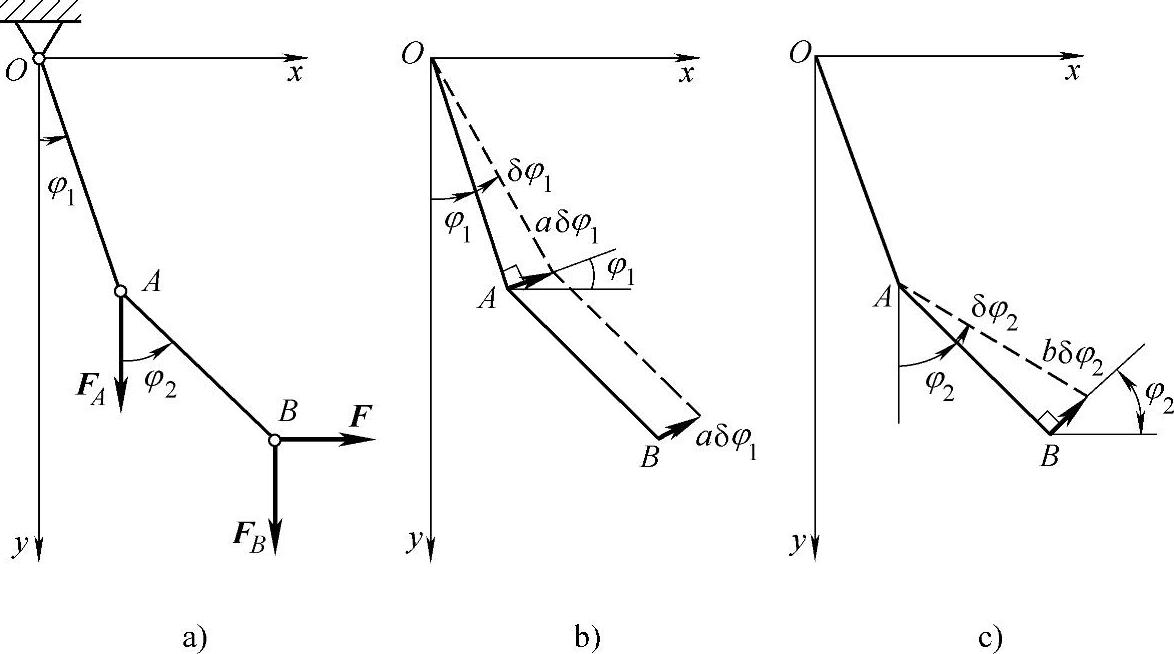
图18-8 例18-1图
已知:OA=a,AB=b,FA,FB,F。
求:φ1,φ2。
解:●建模
杆OA和AB组成的平衡系统受主动力:FA,FB,F。杆OA作定轴转动;杆AB作平面运动。系统的自由度f=2×3-2×2=2。现选择φ1和φ2为系统的两个广义坐标,计算其对应的广义力Q1和Q2。
方法一: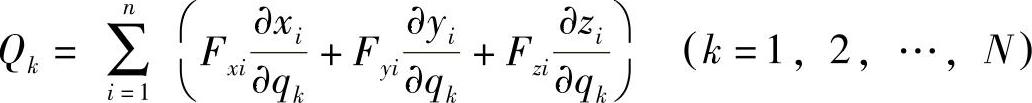
杆OA和AB的位置可由点A和B的4个坐标xA,yA和xB,yB完全确定。xA=asinφ1,yA=acosφ1,xB=asinφ1+bsinφ2和yB=acosφ1+bcosφ2。
●Maple程序

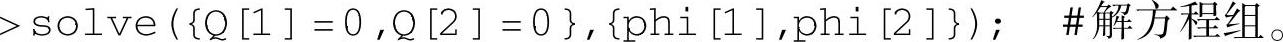
方法二: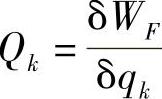 (k=1,2,…,N),保持φ2不变,只有δφ1时,对yA,xB和yB变分可得一组虚位移。保持φ1不变,只有δφ2时,对yA,xB和yB变分可得另一组虚位移。
(k=1,2,…,N),保持φ2不变,只有δφ1时,对yA,xB和yB变分可得一组虚位移。保持φ1不变,只有δφ2时,对yA,xB和yB变分可得另一组虚位移。
●Maple程序

方法三: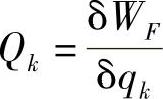 (k=1,2,…,N)。
(k=1,2,…,N)。
直接由几何关系计算给出虚位移。如果保持φ2不变,只有δφ1时,杆AB为平行移动,A,B两点的虚位移相等,可得一组虚位移;如果保持φ1不变,只有δφ2时,点A不动,杆AB为定轴转动,可得另一组虚位移。
●Maple程序


答:平衡时φ1,φ2与FA,FB,F之间的关系为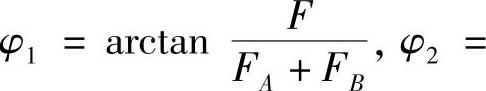
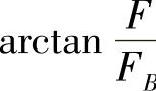 。
。
例18-2 如图18-9所示,重物A和B分别连接在细绳两端,重物A放置在粗糙的水平面上,重物B绕过定滑轮E铅垂悬挂。在动滑轮H的轴心上挂一重物C,设重物A重量为2P,重物B重量为P,不计动滑轮H的重量。试求平衡时重物C的重量PC以及重物A与水平面间的静滑动摩擦因数。
已知:PA=2P,PB=P。
求:PC,fs。
解:●建模
平衡系统受主动力:2P,P,PC,FA。重物A,B,C均作直线运动。系统的自由度f=2。现选择xA和yB为系统的两个广义坐标,计算其对应的广义力QxA和QyB。直接由几何关系计算给出虚位移。如果保持yB不变,只有δxA时,可得一组虚位移;如果保持xA不变,只有δyB时,可得另一组虚位移。
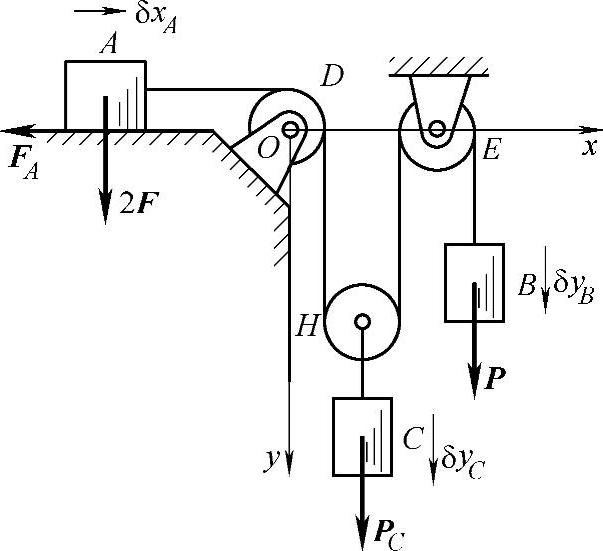
图18-9 例18-2图
●Maple程序


答:平衡时重物C的重量PC=2P,重物A与水平面间的静摩擦因数fs=0.5。
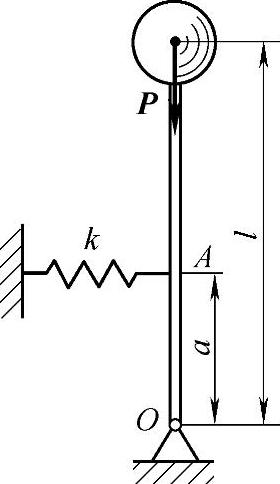
图18-10 例18-3图
例18-3 图18-10所示为一倒置的摆,摆锤重量为P,摆杆长度为l。在摆杆上的点A连有一刚度系数为k的水平弹簧,摆在铅垂位置时弹簧未变形。设OA=a,摆杆重量不计,试确定摆杆的平衡位置及稳定平衡时所应满足的条件。
已知:k,l,P。
求:a。
解:●建模
倒摆平衡系统受主动力:P,Fk。杆OA作定轴转动;倒摆作定轴转动。系统的自由度f=1。选择摆角φ为系统的广义坐标,摆的铅垂位置为摆锤重力势能和弹簧弹性势能的零点,计算系统的总势能。
●Maple程序

答:摆杆的平衡位置为φ=0,稳定平衡时所应满足的条件为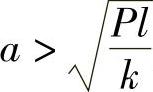 。
。
例18-4 图18-11中,两相同均质圆轮半径皆为R,质量皆为m。轮Ⅰ可绕轴O转动,轮Ⅱ绕有细绳并跨于轮Ⅰ上,当细绳直线部分为铅垂时,求轮Ⅱ中心C的加速度。
已知:m,R。
求:a。
解:●建模
用动力学普遍方程求解。
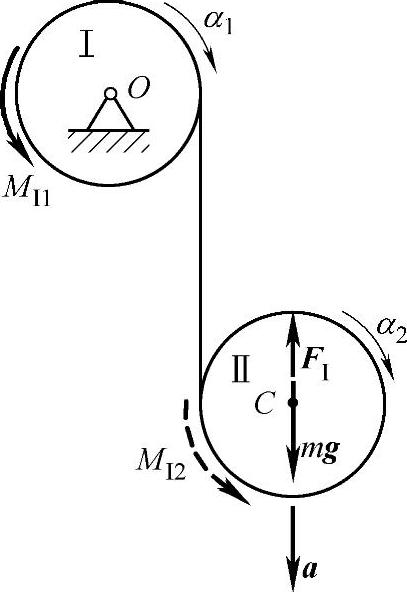
图18-11 例18-4图
整个系统受主动力和惯性力:mg,FⅠ,MⅠ1,MⅠ2。轮Ⅰ作定轴转动;轮Ⅱ作平面运动。系统的自由度f=3×2-2-1=3。水平方向质心坐标守恒。选择轮Ⅰ、轮Ⅱ的转角φ1,φ2为系统的广义坐标。设轮Ⅰ,Ⅱ的角加速度分别为α1,α2,轮Ⅱ质心C的加速度为a。惯性力FⅠ,MⅠ1,MⅠ2的大小分别为FⅠ=ma,MⅠ1=JOα1,MⅠ2=JCα2。(https://www.daowen.com)
●Maple程序


答:轮Ⅱ中心C的加速度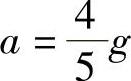 。
。
例18-5 在图18-12所示的运动系统中,重物M1的质量为m1,可沿光滑水平面移动;摆锤M2的质量为m2。两个物体用无重杆连接,杆长为l。试建立此系统的运动微分方程。
已知:m1,m2,l。
求:建立系统运动微分方程。
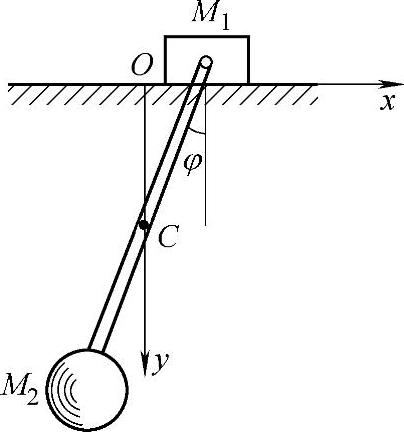
图18-12 例18-5图
解法一:●建模
利用第一类拉格朗日方程。整个系统受主动力:m1g,m2g。重物M1作直线运动;摆锤M2作平面运动。系统的自由度f=3+2-2-1=2。设质点M1的坐标为x1,y1,质点M2的坐标为x2,y2。
注:关于第一类拉格朗日方程的概念,详见参考文献[10]。
●Maple程序


答:此系统的运动微分方程为
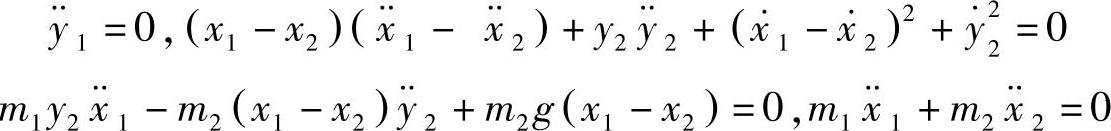
解法二:●建模
利用第二类拉格朗日方程。
整个系统所受的主动力均为有势力。重物M1作直线运动;摆锤M2作平面运动。系统的自由度f=2。选x1和φ为广义坐标,则有y1=0,x2=x1-lsinφ,y2=lcosφ。选地面为系统的零势能位置。
●Maple程序



答:此系统的运动微分方程为
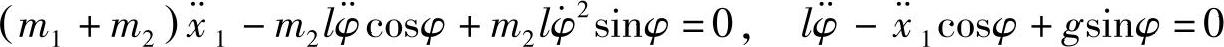
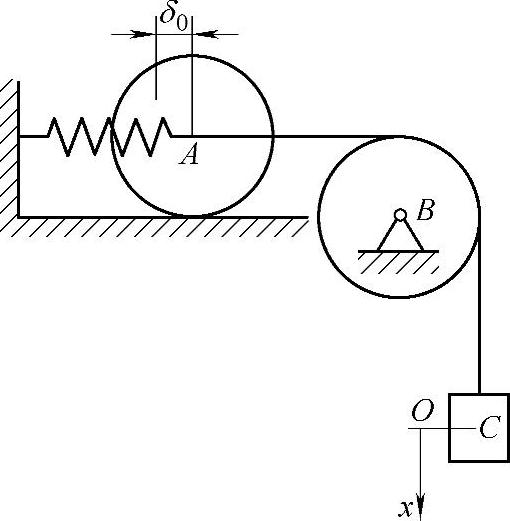
图18-13 例18-6图
例18-6 图18-13所示的系统中,轮A沿水平面纯滚动,轮心以水平弹簧连于墙上,质量为m1的物块C以细绳跨过定滑轮B连于点A。A,B两轮皆为均质圆盘,半径为R,质量为m2。弹簧刚度系数为k,质量不计。当弹簧较软,在细绳能始终保持张紧的条件下,求此系统的运动微分方程。
已知:m1,m2,k,R。
求:建立系统运动微分方程。
解:●建模
利用第二类拉格朗日方程。整个系统所受的主动力均为有势力。物块C作直线运动;圆盘A作平面运动;圆盘B作定轴转动。系统的自由度f=1。取x为广义坐标。以平衡位置为重力势能点,取弹簧原长处为弹性力零势能点。
●Maple程序


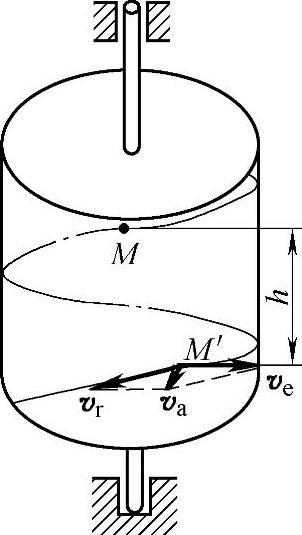
图18-14 例18-7图
答:系统的运动微分方程为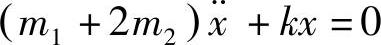 。
。
例18-7 图18-14所示为一均质圆柱体,可绕其铅垂中心轴自由转动。圆柱表面上刻有一倾角为θ的螺旋槽。今在槽中放一小球M,自静止开始沿槽下滑,同时使圆柱体绕轴线转动。设小球质量为m1,圆柱体的质量为m2,半径为R,不计摩擦。求当小球下降的高度为h时,小球相对于圆柱体的速度,以及圆柱体的角速度。
已知:m1,m2,h,R,θ。
求:vr,ω。
解:●建模
利用拉格朗日方程的初积分。小球和圆柱体组成的系统所受的主动力均为有势力,并具有稳定、完整、理想约束,所以是保守系统。小球M作曲线运动;均质圆柱体作定轴转动。系统的自由度f=2。取均质圆柱体的转角φ和沿螺旋槽方向的弧坐标s为广义坐标。选择小球起点为零势能点。
●Maple程序


答:当小球下降的高度为h时,小球相对于圆柱体的速度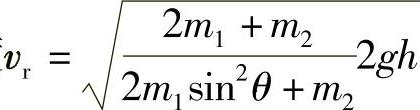 ,圆柱体的角速度
,圆柱体的角速度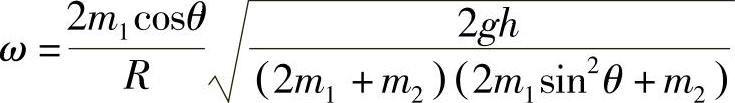 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







