设拉格朗日函数L不是时间的显函数，则

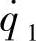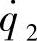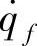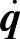这里已把q₁，q₂，…，q_f缩写为q，把，，…，缩写为。由此∂L/∂t=0，从而L的时间变化率

在主动力全是势力的情况下，利用拉格朗日方程（18-21）把∂L/∂q_j改写，即得

式中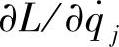，就是广义动量p_j，这样

定义哈密顿函数

则式（18-27）就是哈密顿函数守恒原理，即

弄清楚哈密顿函数的意义，显然是很重要的。势能V是与广义速度无关的，因此H的定义式（18-27）中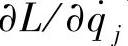可代之以。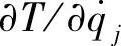

设变换式r_i=r_i（q）不显含时间，即∂r_i/∂t=0，于是由式（18-17），得

这是广义速度的二次齐次多项式。根据齐次函数的欧拉定理，得

由此，哈密顿函数

这样，在变换式r_i=r_i（q）不显含时间的条件下，哈密顿函数H就是机械能。

设系统满足下面条件：

1）双向，理想约束的完整定常系统，r_i=r_i（q）；

2）系统所有主动力有势，；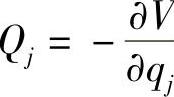

3）势能不显含时间，即V=V（q），满足这些条件的系统称为保守系统。对该系统有

即保守系统的机械能在运动中保持不变，系统有能量积分

E=T+V=H=const （18-30b）

如果约束是非定常的，则变换式r_i=r_i（q，t）必然显含时间t，即使约束是定常的，也可能由于选择了某些广义坐标（例如平行移动坐标系），在变换式r_i=r_i（q，t）显含时间t的情况下，由式（18-15）

T=T₂+T₁+T₀ （h）(www.daowen.com)

根据齐次函数的欧拉定理，得

由此，哈密顿函数

这样，在变换式显含时间的条件下，哈密顿函数H并非机械能，只能称之为广义能量。仅用哈密顿函数表示的动力系统称为哈密顿系统。在哈密顿系统中具有广义能量守恒定律

T₂-T₀+V=h （18-32）

式中，h是任意常数。式（18-32）称为雅可比积分。

习题8 质量为m、半径为r的圆环在圆心A上铰接一长度为l、质量亦为m的单摆B，如图示18-7所示。试就以下两种情况讨论拉格朗日方程的初积分：

（1）圆环作纯滑动；

（2）圆环作纯滚动。

图 18-7

解：此系统的自由度数为2，以圆环中心A的坐标x和摆偏角θ为广义坐标。

（1）圆环作纯滑动 以过圆环中心A的平面为零势能面，系统的拉格朗日函数为

L中不显含x，存在循环积分

其物理意义为沿x轴方向的动量守恒。L中不显含时间t，且约束为定常，存在能量积分

（2）圆环作纯滚动 系统的拉格朗日函数为

系统的循环积分改为

虽然广义动量守恒，但按矢量力学观点，由于接触处存在摩擦力，系统沿x轴的动量不守恒。系统的能量积分改为

广义动量守恒，或循环积分，可以是对固定轴的动量守恒，如式（4）和式（10）；可以是对固定轴的动量矩守恒，如式（2）和式（8）；可以是对动轴的动量矩守恒，如式（5）和式（7）；可以不是动量守恒，如式（13）。