如果拉格朗日函数L不包含某个广义坐标q_k，即∂L/∂q_k=0，这种广义坐标叫做循环坐标（或可忽略坐标）。于是，拉格朗日方程（18-21）给出

这就是说，广义动量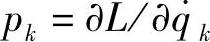是守恒的，即

这叫做广义动量守恒原理。

如果q_k是力学系统的整体平行移动坐标，则广义动量守恒原理就归结为本书Ⅰ册的动量守恒原理。如果q_k是力学系统的整体转动坐标，则广义动量守恒原理就归结为本书Ⅰ册的动量矩守恒原理。但是本书Ⅰ册论述动量守恒原理和动量矩守恒原理时以牛顿第三定律为先决条件（内力的矢量和为零，内力的力矩和为零），而广义动量守恒原理则并不以牛顿第三定律为先决条件。

广义动量可以是系统的动量，可以是系统的动量矩，也可以既不是动量也不是动量矩。因此，广义动量守恒，或者表示动量守恒，或者表示动量矩守恒，或者不是上述两种守恒。这里动量矩可以是对固定轴的，也可以是对动轴的。

习题5 质点在有心力作用下的运动。

解：系统的拉格朗日函数为

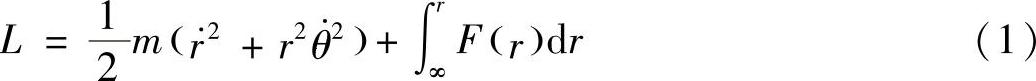
其中，r，θ为质点的极坐标。θ为循环坐标，有循环积分

它代表对过力心的固定轴的动量矩守恒。

习题6 质量为m₁的平板放在光滑平面上，平板上放一质量为m₂、半径为R的圆盘，圆盘可沿平板作纯滚动（图18-5）。

解：系统的拉格朗日函数为

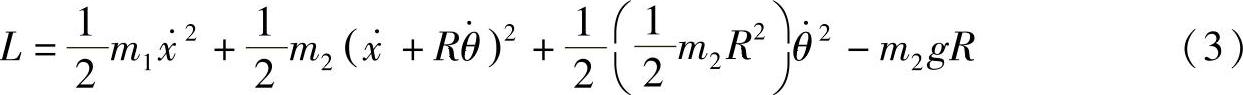(www.daowen.com)

其中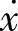，为平板速度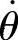，为圆盘角速度。由式（3）知，x，θ为循环坐标，因此有循环积分

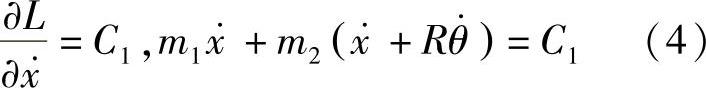
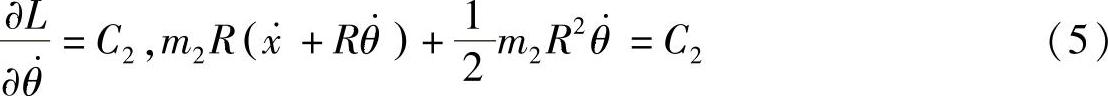
积分式（4）代表系统对固定轴Ox的动量守恒，而积分式（5）代表系统对过接触点A垂直于所在平面的动轴的动量矩守恒。

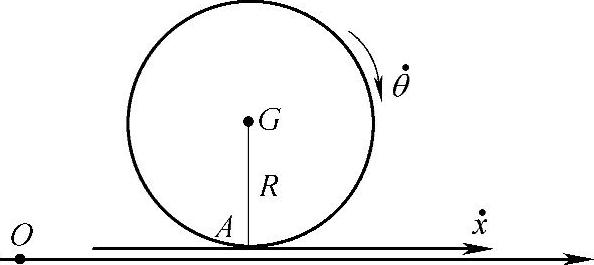
图 18-5

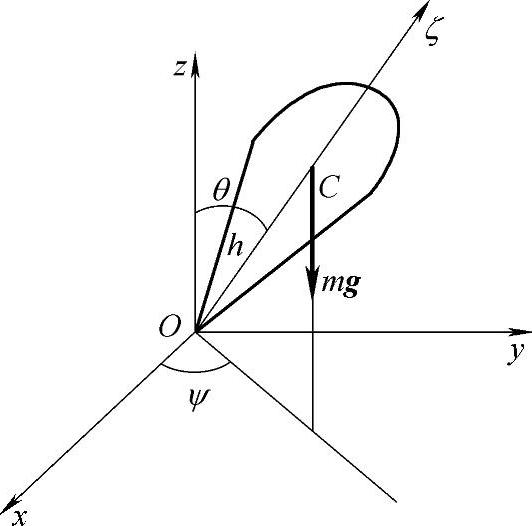
图 18-6

习题7 拉格朗日陀螺如图18-6所示，陀螺绕定点O转动。

解：拉格朗日函数有如下形式（利用式（22-22））：

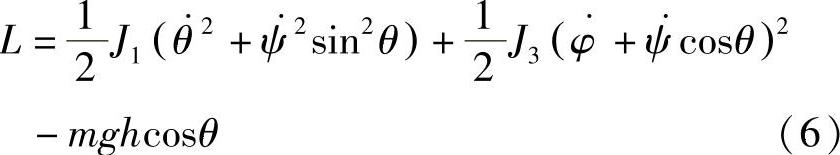
其中，ψ，θ，φ为欧拉角，J₁，J₃为陀螺在点O的主惯性矩。由式（6）知，φ和ψ为循环坐标，因此有循环积分

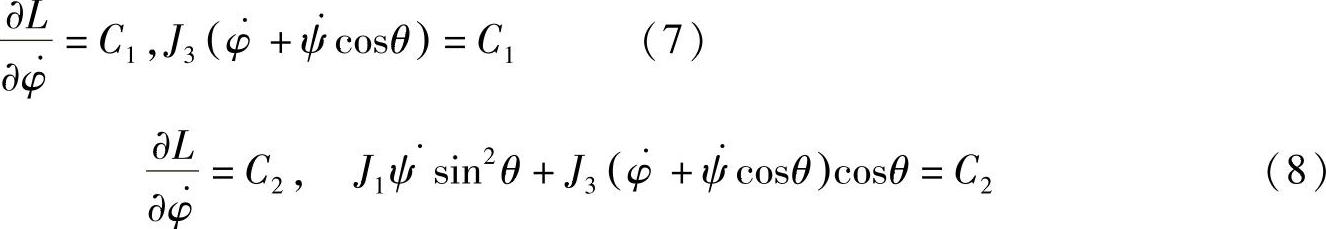
积分式（7）代表系统对动轴Oζ的动量矩守恒，而积分式（8）代表系统对过固定轴Oz的动量矩守恒。