如果主动力有势,设广义力Qj由下面公式计算:
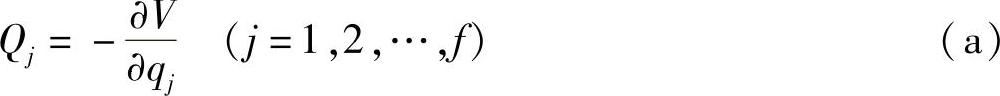
式中,势能V=V(q1,q2,…,qf,t)。
拉格朗日方程(18-11)在有势力情况下写成为
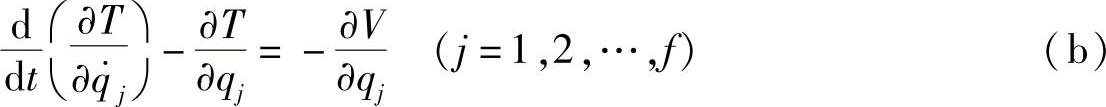
令L=T-V,那么上面方程写成为
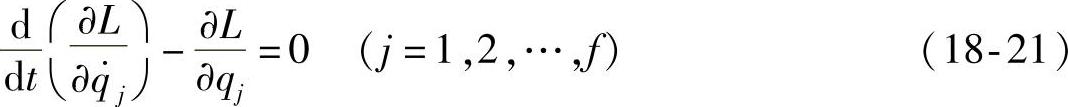
函数L称为拉格朗日函数。方程(18-21)适用于理想双向约束的完整有势系统。仅用拉格朗日函数就可以表示的动力系统称为拉格朗日系统。
利用式(18-15),拉格朗日函数是广义速度的二阶多项式,可以写成为
L=L2+L1+L0 (18-22a)式中,
L2=T2,L1=T1,L0=T0-V (18-22b)
于是列写质点系的运动微分方程归结为写出质点系的拉格朗日函数L。一般情况下,L是qj,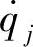 (j=1,2,…,f)和t的函数:
(j=1,2,…,f)和t的函数:
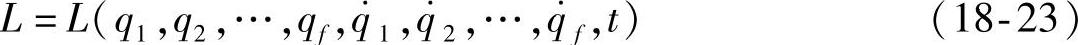
由于函数L完全确定质点系的运动规律,因此,可将拉格朗日函数称为质点系的特征函数。
L对广义坐标的偏导数

L对广义速度的偏导数
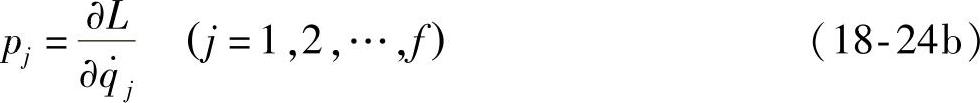
的量纲为动量或动量矩的量纲,称为广义动量。
试求下面在均匀重力场(重力加速度为g)中各系统的拉格朗日函数。
习题1 平面双摆(图18-1)。
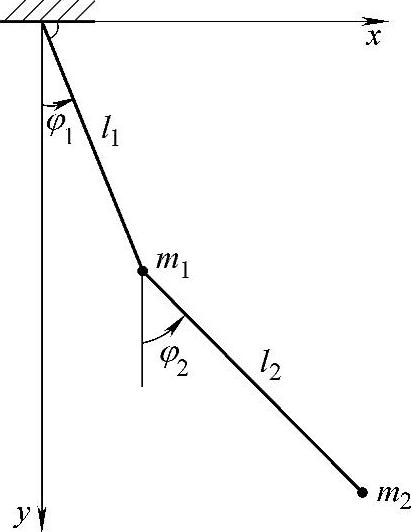
图18-1 平面双摆
解:取绳l1和l2分别与竖直方向的夹角φ1和φ2为广义坐标。对质点m1有
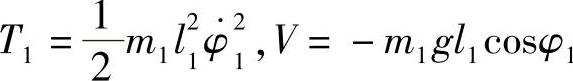
为了求出第二个质点的动能,我们用角φ1和φ2表示第二个质点的笛卡儿坐标x2,y2(坐标原点取在悬挂点,y轴竖直向下):
x2=l1sinφ1+l2sinφ2,y2=l1cosφ1+l2cosφ2
于是有
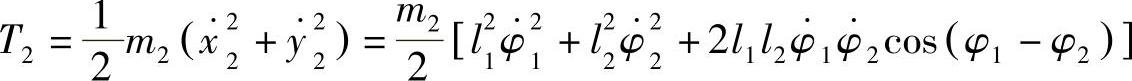
最后得(www.daowen.com)
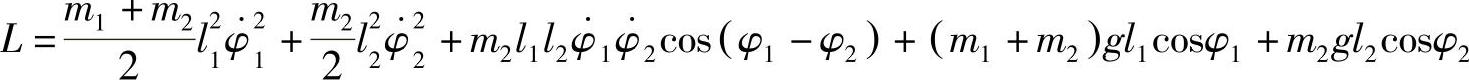
习题2 质量为m2的平面摆,其悬挂点(质量为m1)可以沿着水平直线运动(图18-2)。
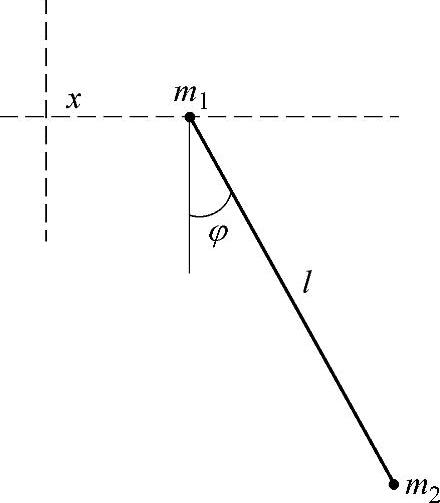
图18-2 平面摆
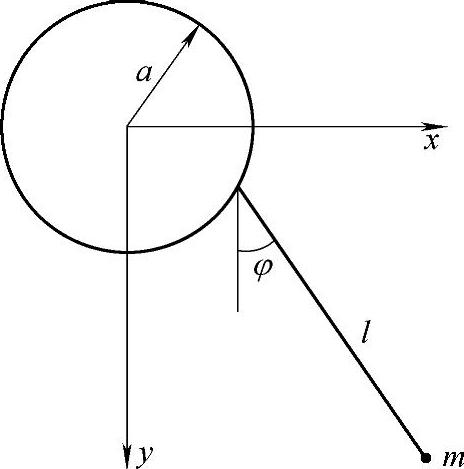
图18-3 悬挂点作圆周运动的平面摆
解:设质点m1的坐标为x,绳与竖直方向夹角为φ,则有
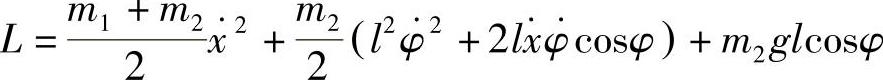
习题3 设有一平面摆,其悬挂点:
(1)沿着竖直圆以定常圆频率Ω运动(图18-3);
(2)按规律acosΩt水平振动;
(3)按规律acosΩt竖直振动。
解:(1)质点m的坐标为
x=acosΩt+lsinφ,y=-asinΩt+lcosφ拉格朗日函数为
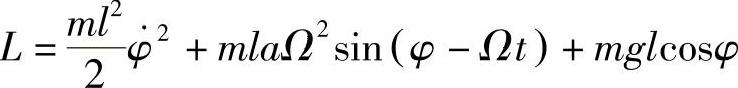
这里略去了仅仅依赖于时间的项,它可以写成mlaΩcos(φ-Ωt)对时间的全导数。
(2)质点m的坐标为
x=acosΩt+lsinφ,y=lcosφ拉格朗日函数(略去全导数)为
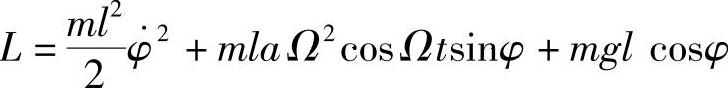
(3)类似地,可得
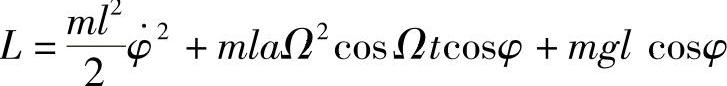
习题4 在图18-4所示的力学系统中,质点m2沿着竖直轴运动,整个系统以常角速度Ω绕该轴转动。
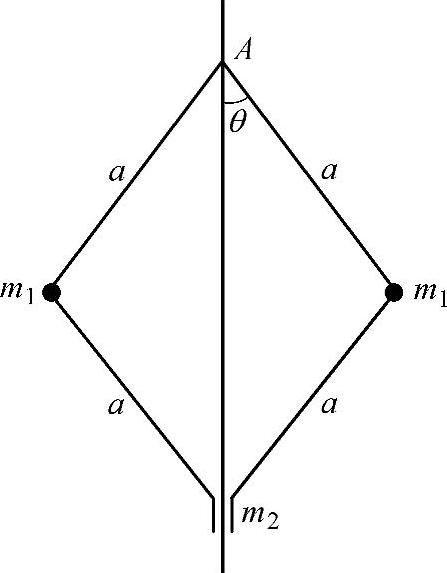
图 18-4
解:设线段a与竖直方向夹角为θ,系统绕竖直轴转动的角度为φ,则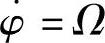 。对于每个质点m1的微小位移有
。对于每个质点m1的微小位移有
dl21=a2dθ2+a2sin2θdφ2
质点m2到A点的距离为2acosθ,因此
dl2=-2asinθdθ
拉格朗日函数为
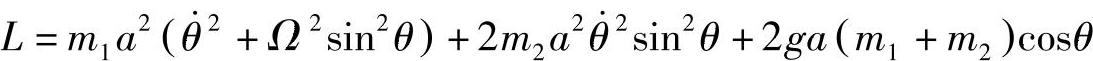
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







