我们研究由n个质点P_i（i=1，2，…，n）组成的系统。如果系统是非自由的，则约束是双向理想的。设质点P_i的虚位移为δr_i，质量为m_i，加速度为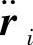，而F_i是作用在质点P_i上的主动力的合力，那么动力学普遍方程（17-43）写成为

在某些约束或者全部约束非理想的情况下，把非理想约束力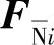当成主动力F_i处理，就可以在形式上与理想约束系统一样来研究。

动力学普遍方程（18-1）是我们推导分析动力学微分方程的基础，实际上，所有的质点系运动方程都是式（18-1）的不同形式，对应于不同性质的主动力和约束。

设系统有r个几何约束和s个不可积的微分约束，并设q_j（j=1，2，…，m）是系统的广义坐标，其数目m=3n-r，那么质点相对于惯性坐标系原点的矢径r_i可以写成q₁，q₂，…，q_m，t的函数形式，即

r_i=r_i（q₁，q₂，…，q_m，t） （i=1，2，…，n） （18-2）这些函数是二次连续可微的。如果系统是定常的，则可以选择广义坐标q₁，q₂，…，q_m使函数r_i不显含时间t。由式（18-2）可得

我们将动力学普遍方程（18-1）写成广义坐标的形式，主动力的虚功形式为

式中，Q_j是主动力对应于广义坐标q_j的广义力，一般是q_l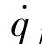，l，t（l=1，2，…，m）的函数，即

我们再对惯性力在虚位移上所做的功的表达式进行变换。利用式（18-4），改变求和次序，得

又(www.daowen.com)

借助两个恒等式即式（17-24）和式（17-25）可将上式写成为

如果利用系统动能表达式

则等式（b）可以写成为

将式（18-8）代入式（18-7）可得惯性力虚功表达式

引入广义惯性力

将式（18-5）和式（18-9）代入式（18-1）得广义坐标形式的动力学普遍方程

定理（广义坐标形式的达朗贝尔-拉格朗日原理）对理想双向约束的系统，在给定时刻的所有可能运动中，只有真实运动使主动力对应的广义力和惯性力对应的广义力在广义虚位移上的虚功之和等于零。