1.高斯原理（最小拘束原理）的公式

我们将在某时刻具有可能位置r_i^∗和可能速度v_i^∗的运动同真实运动相比较。

被比较的可能运动的加速度是不同的（它们之差不一定是无穷小量）。这种等时变分的方法称为高斯变分。如果将两个运动学可能运动的加速度之差用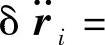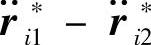表示，则由式（17-19）知

将这个虚位移表达式（d）代入动力学普遍方程（17-43），并消去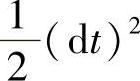得

这里我们采用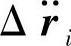代替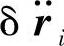，从而体现这个值不一定是无穷小量。也可以写成标量形式：

注意到m_i是常数，而力F_i不依赖于加速度，方程（17-45）可以写成为

δZ=0 （17-46）

式中，

称为拘束。(www.daowen.com)

高斯原理（最小拘束原理）：对理想双向约束的系统，在给定时刻的可能运动（r^∗_i1=r_i2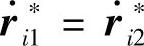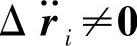^∗，，）中，真实运动的拘束最小。

证明：根据式（17-46）可知，可能加速度的函数Z在真实运动的加速度处取驻值。函数Z在真实运动的加速度处不仅取驻值，而且取最小值。事实上，设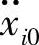为系统真实运动的加速度分量，而Z₀是相应的拘束值，那么，假设在真实运动相比较的运动学可能运动中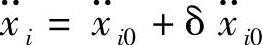，于是有

根据方程（17-45b），式（17-48）右端第1个求和等于零。由于不是所有的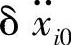（i=1，2，…，3n）都等于零，因此式（17-48）右端第2个求和是严格正的，因此Z在真实运动的加速度处取最小值。

达朗贝尔-拉格朗日变分原理和若尔当变分原理不涉及极值的概念。高斯提出了达朗贝尔-拉格朗日原理的显著变异，引入了某个表达式的最小值概念。达朗贝尔-拉格朗日原理的这个变异称为高斯原理或者最小拘束原理。

2.高斯原理的物理意义

高斯原理的物理意义可以把拘束广义地理解为约束。考虑到式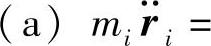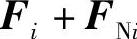，我们可以将拘束表达式写成为

Z真实运动取最小值的条件变为约束力的极值性质：真实运动的约束力最小（意思是式（17-49）取最小值）。