设q₁，q₂，…，q_m是系统的广义坐标，Q_j=Q_j（q，t）（j=1，2，…，m）是相应主动力的广义力，方程（17-32）的广义坐标形式为

这就是广义坐标下的静力学普遍方程。

定理 （虚位移原理）具有理想双向约束的质点系平衡的充分必要条件是：所有主动力与广义坐标（在平衡位置）对应的广义力在广义虚位移上所做的虚功之和等于零。

1.完整系统中的静力学普遍方程

如果系统是完整的，则广义坐标数m等于自由度f，即m=f，且方程（17-34）中的δq_j是独立的。令方程（17-34）中δq_j的系数等于零，可得系统在平衡位置q=q₀（只有在该位置）主动力的广义力等于零，即

Q_j=0 （j=1，2，…，f） （17-37）这就是完整系统中的静力学普遍方程。式（17-37）构成了关于未知数q₁₀，q₂₀，…，q_f0的f个方程，这些未知数确定了系统的平衡位置。

定理 受理想双向约束的完整系统，其平衡的充分必要条件为：所有主动力与广义坐标（在平衡位置处）对应的广义力均等于零。

2.势力场中的静力学普遍方程

如果所有的主动力都有势，则根据式（17-35），并由方程（17-37）得

式中，V是系统的势能。由此可知：

定理1 完整系统（受双向理想约束，在有势力场中）在某位置平衡的充分必要条件就是系统（在该位置）势能取驻值。即势能取极值的必要条件。(www.daowen.com)

特别地，如果系统在均匀重力场中运动，则条件方程（17-38）可以变为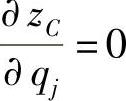（j=1，2，…，f），其中z_C是系统重心在以Oz为铅垂轴的固定坐标系的坐标，即系统平衡的充分必要条件就是系统重心高度取极值的必要条件。

进一步的研究可以证明：

定理2 （拉格朗日-狄利克雷定理）受双向理想约束，在有势力场中的完整系统，若质点系在平衡位置上的势能具有极小值，则该平衡位置是稳定的。

3.非完整系统中的静力学普遍方程

如果系统是非完整的，则方程（17-36）中的δq_j不是独立的，它们满足s个约束方程（17-29），在m个δq_j中只有f（f=m-s）个独立。为了确定性假设δq_i（i=1，2，…，f）独立，从方程（17-29）中解出δq_f+1，δq_f+2，…，δq_m得

式中，α_kl=f（b_kj），b_kj是方程（17-29）中的系数。在方程（17-36）中代入表达式（17-39）后合并同类项得

式中，

由于δq_i（i=1，2，…，f）独立，由式（17-40）可得

Q′_i=0 （i=1，2，…，f） （17-42）

式（17-42）是关于m个未知数q₁₀，q₂₀，…，q_m0的f个方程，这些未知数确定了系统的平衡位置。由于位置数的个数超过方程数，因此一般来说可以得到平衡状态流形，其维数不小于非完整约束的数目s。从方程（17-41）和方程（17-42）可以看出，对于在有势力场中的非完整系统，势能的某些甚至全部导数在平衡位置都可以不等于零。