1.自由度

虚位移δx_i，δy_i，δz_i（i=1，2，…，n）满足由r+s个方程组成的方程组（17-9）和方程组（17-10）独立的虚位移数目称为系统的自由度。今后我们总是用f表示自由度。显然

f=3n-r-s （17-20）

例9 一个质点在空间中运动有3个自由度。

例10 两个质点用杆连接在平面上运动有3个自由度（图17-7）。

例11 冰刀（图17-1）有2个自由度。

例12 沿着固定或运动曲面运动的质点有2个自由度。

例13 两个杆用柱铰链相连在平面内运动（剪刀）有4个自由度。

2.广义坐标

我们研究有约束式（17-1）、式（17-2）的非自由质点系，假设r个关于3n个变量x_i，y_i，z_i（i=1，2，…，n）的函数f_k是相互独立的（这里时间t看做参数），反之，约束中一定有一个是与其他矛盾的或者可以从其他得到的。

确定系统可能位置的参数的最小数目称为独立广义坐标数，因为函数f_k（k=1，2，…，r）是相互独立的，广义坐标数（用m表示）等于3n-r。广义坐标可以从3n个笛卡儿坐标x_i，y_i，z_i中选取m个，使得方程（17-1）相对它们可以解出。然而一般来说，这样选择广义坐标的方法在实践中很少使用。可以选取任意m个独立的可以确定系统位形的量q₁，q₂，…，q_m，它们可以是距离、角度、面积，也可以是没有直接几何意义的，只需要相互独立并且可以将笛卡儿坐标r_i，x_i用q₁，q₂，…，q_m和t表示出来：

r_i=r_i（q₁，q₂，…，q_m，t） （i=1，2，…，n） （17-21a）

x_i=x_i（q₁，q₂，…，q_m，t） （i=1，2，…，3n） （17-21b）

将这些函数代入式（17-1）后，得到完整系统约束恒等式：

g_k（q₁，q₂，…，q_m，t）=0 （k=1，2，…，r） （17-22）矩阵

的秩等于m。由此可知，在式（17-21）的3n个关于q₁，q₂，…，q_m的函数（t为参数）x_i中，有m个独立，用它们可以表示出系统的其他坐标。

我们假设选择广义坐标q₁，q₂，…，q_m，使得系统的任意可能位置都可以在q₁，q₂，…，q_m取某些值时利用式（17-21）得到。如果不能得到所有可能位置，则局部地引入广义坐标，即对于不同的可能位置集合引入不同的广义坐标。

我们假设函数（17-21）对其所有自变量都是二阶连续可微的。此外，我们认为，如果系统是定常的，则通过选择广义坐标总是可以使时间t不显含在关系式（17-21）中。

在研究具体问题时，经常完全不需要建立约束方程（17-22），根据问题的物理意义就能知道，确定系统可能位置所必需的广义坐标数量。如果解题时需要关系式（17-22）可以借助几何意义建立。

3.广义坐标空间

对于每个时刻t，系统的可能位置和m维空间（q₁，q₂，…，q_m）之间一一对应，空间（q₁，q₂，…，q_m）称为坐标空间（或构形空间）。系统的每个可能位置对应于坐标空间中的某个点，该点称为映射点。系统的运动对应于映射点在坐标空间中的运动。

坐标空间中点的距离自然地用系统相应的位置之间的距离定义，这样，在系统位置和坐标空间的点之间存在着连续的一一对应关系。

例14 质点在平面上运动，坐标空间就是这个平面。

例15n个自由质点在空间中运动，坐标空间是3n维欧氏空间。

图17-5 单摆

例16（单摆） 将单摆看做一端固定不动的刚性杆，单摆的位置用广义坐标角φ确定（图17-5），将单摆的每个位置对应于坐标为φ的数轴上的点。由于数轴上不同的点φ和φ+2kπ（k=±1，±2，…）对应着单摆的同一个位置，因此单摆位置和数轴上的点不是一一对应的。从数轴上划分出的一个半开区间0≤φ<2π可以实现与单摆位置的一一对应。但这样破坏了连续性，因为单摆的两个邻近位置φ=0和φ=2kπ-ε不是半开区间的邻近点。为了保证连续性，需要认为φ=0和φ=2kπ是同一个点。直观地可以这样做：“粘接上”φ=0点和φ=2kπ点，得到的几何形状——圆就是单摆的坐标空间。

例17（双摆） 由两个刚性杆用柱铰链连接，一个杆的自由端悬挂于固定点A（图17-6），另一个杆可以在一个平面内自由运动。广义坐标可以取两个杆与竖直方向的夹角φ和ψ，双摆的每个位置对应于两个不超过2π的数φ和ψ，因此如果我们取φ，ψ平面上边长为2π的正方形，并认为对边是同一条线段，则得到双摆的坐标空间。直观地可以这样做：“粘接上”正方形的对边，第一次粘接得到圆柱，此后第二次粘接得到的几何形状是圆环。(www.daowen.com)

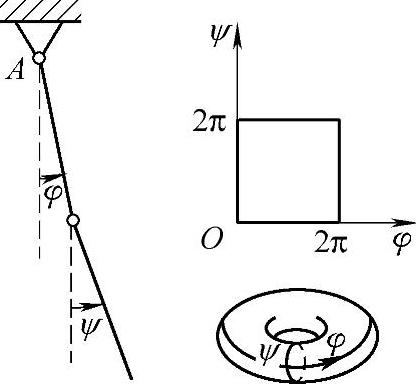
图17-6 双摆

例18 用杆连接的两个质点在平面上运动（图17-7），广义坐标可以取一个点的笛卡儿坐标x，y和杆与Ox轴的夹角φ；坐标空间是空间（x，y，φ）中的一层，用平面φ=0和φ=2kπ分割开来，并认为这两个平面是同一个。这里与实例15和实例16不同的是，无法直观地“粘接上”平面φ=0和φ=2kπ。

图17-7 刚体的平面运动

4.广义速度和广义加速度

在系统运动时广义坐标随时间变化，和（j=1，2，…，m）称为广义速度和广义加速度。利用微分复合函数（17-21）可以求出系统各点速度加速度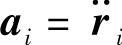和可能位移dr_i的笛卡儿坐标形式：

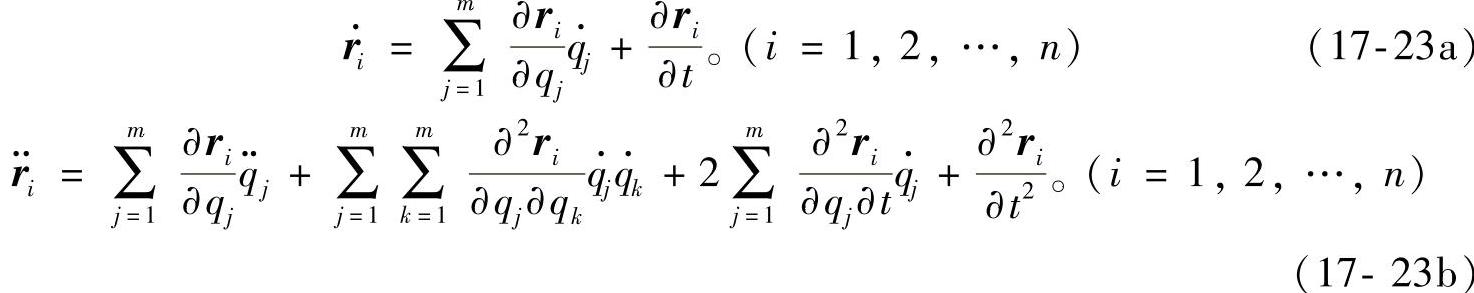
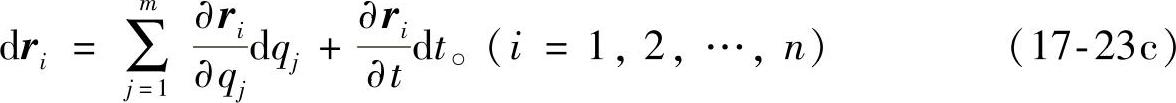
这里给出后面会用到的两个等式：

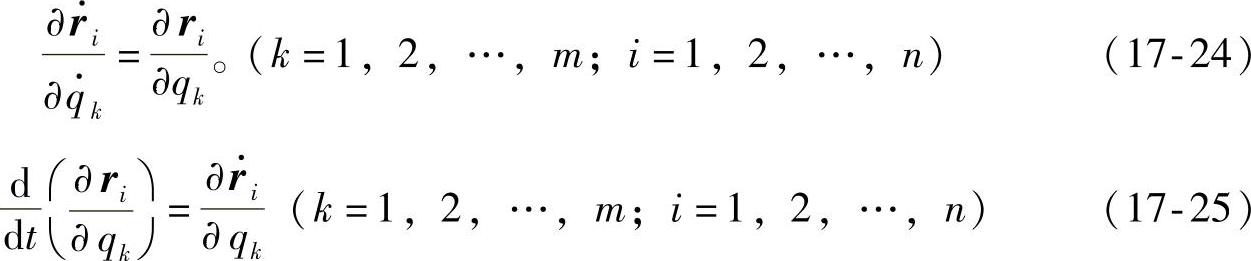
证明：第1个等式直接从式（17-23a）就可以得到。利用式（17-23a）以及函数r_i对其自变量微分的顺序可交换，第2个等式容易通过微分推导出。因为假设函数r_i是二阶连续可微的，微分可交换性成立，于是得

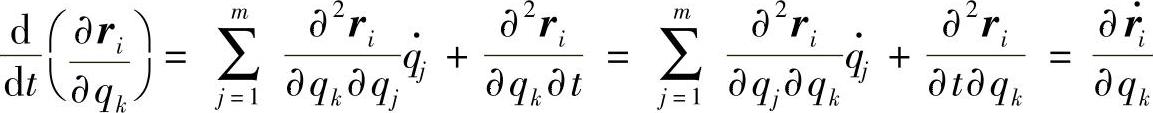
我们下面将非完整约束方程（17-2）写成广义坐标形式。将式（17-21b）和式（17-23）代入式（17-2）得

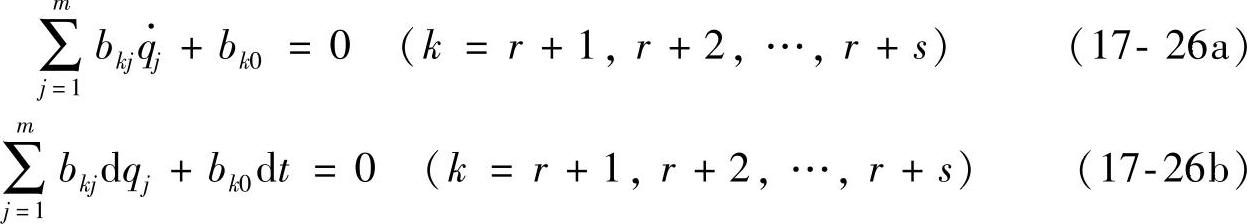
其中，b_kj=b_kj（q₁，q₂，…，q_m，t），b_k0=b_k0（q₁，q₂，…，q_m，t）由下面等式确定：

这里的a_ki，a_k0中的x₁，x₂，…，x_3n利用式（17-21b）作了代换。

不论是完整系统还是非完整系统，广义坐标q_j（j=1，2，…，m）相互独立并且可以任意取值。对于完整系统，广义速度相互独立并且可以任意取值；但对于非完整系统，广义速度不是独立的，它们受s个关系式（17-26a）的限制。

对于完整系统，dq_j相互独立并且可以任意取值；但对于非完整系统，dq_j不是独立的，它们受s个关系式（17-26b）的限制。

5.用广义坐标表示的虚位移

引入δq_j（j=1，2，…，m）为广义坐标的等时变分，即同一时刻、同一位置两组广义坐标微分之差

δq_j=dq_j（1）-dq_j（2）。（j=1，2，…，m） （17-27）

根据式（17-23c），选择两组可能位移相减可得

对于完整系统，δq_j相互独立并且可以任意取值；但对于非完整系统，δq_j不是独立的，它们受如下s个关系式的限制，即

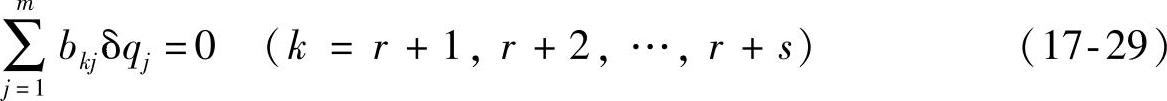
由此可知，完整系统的自由度f与广义坐标数m相等，即f=m；非完整系统的自由度f小于广义坐标数m，即f<m，在数量上少了不可积微分约束的个数，则f=m-s。