1.真实位移

一般来说，真实位移是实际发生的无穷小位移，质点系满足动力学基本定律，初始条件和约束条件的无穷小位移称为真实位移。我们把质点系满足运动微分方程，初始条件r_i（t₀）=r_i0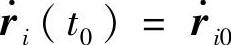，和约束条件式（17-7）和式（17-8）与dt呈线性关系的无穷小位移，称为真实位移。真实位移是可能位移的一个。

2.虚位移

一般来说，质点系在约束允许的条件下，与∙时∙间∙的∙变∙化∙Δt=dt无∙关∙的微小位移称为虚位移。设在时刻t=t^∗处于矢径r_i^∗确定的某个位置，我们把虚位移定义为满足下面线性齐次方程组的δr_i=δr_i^∗（i=1，2，…，n）集合：

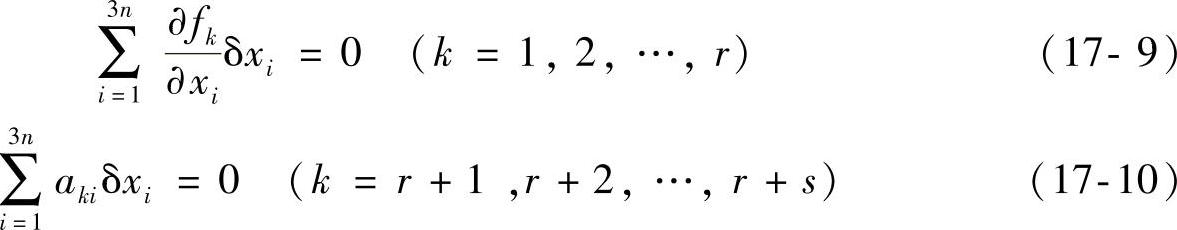
这里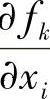，aki是在t=t^∗，r_i=r_i^∗时计算的，均为x_i（i=1，2，…，3n）和t的函数。

设δr_i的分量为δx_i，δy_i，δz_i，因为3n-r-s₁>0，即未知数δx_i，δy_i，δz_i（i=1，2，…，n）的数目大于它们必须满足的方程组（17-9）和方程组（17-10）的个数，所以存在无穷多个虚位移δr_i^∗。

3.真实位移、可能位移和虚位移的关系

对于具有双向、定常约束的完整系统，可能位移满足的方程（17-7）变成为

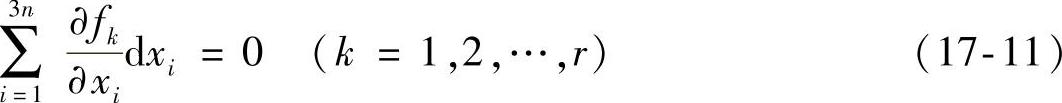
这里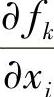为x_i（i=1，2，…，3n）的函数。比较式（17-9）和式（17-11），可能位移的集合与虚位移集合完全相同。由此可知：对于具有双向、定常约束的完整系统真实位移是虚位移之一。

例8 对于斜面固定和作平行移动两种情形，分析沿斜面运动质点的可能位移和虚位移。

解：斜面固定时，质点的可能位移和虚位移相同（图17-4a）。斜面作已知规律的平行移动时，质点的可能位移应考虑牵连运动的影响，而质点的虚位移等于约束凝固时的可能位移，与斜面固定时的可能位移相同（图17-4b）。

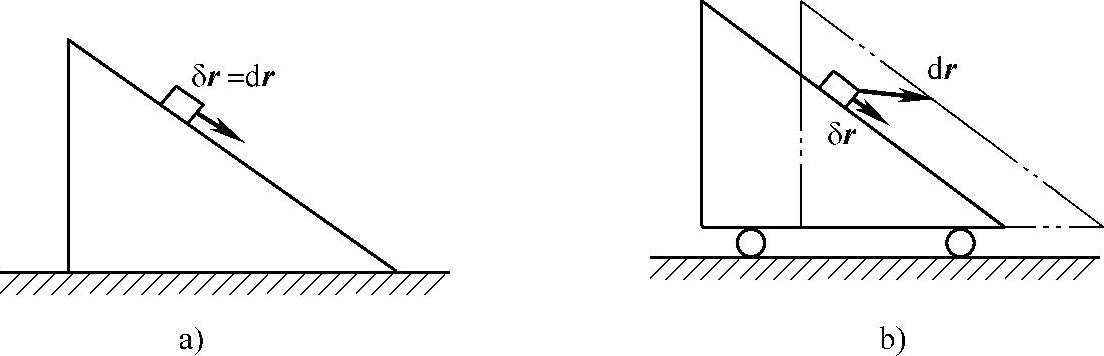
图17-4 实例8图

a）斜面固定 b）斜面平行移动

对于具有双向、速度齐次约束的非完整系统，可能位移满足的方程（17-8）变成为

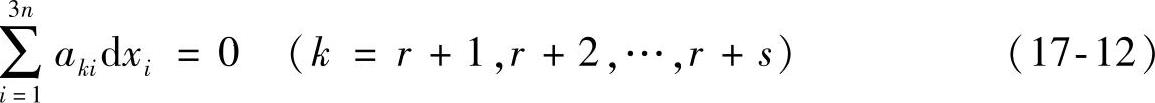
这里a_ki为x_i（i=1，2，…，3n）和t的函数。比较式（17-10）和式（17-12），可能位移的集合与虚位移集合完全相同。由此可知：对于具有双向、速度齐次约束的非完整系统真实位移是虚位移之一。

对于例7中，实位移dx，dy满足：

dy-tdx=0 （e）

虚位移δx，δy满足：

δy-tδx=0 （f）

比较式（e）与式（f）可知，虽然约束是非定常的，但真实位移是虚位移中的一个。(www.daowen.com)

4.等时变分

无穷小增量δx_i，δy_i，δz_i称为x_i，y_i，z_i的变分。在t=t^∗固定时，从矢径r_i^∗确定的位置，变化到无限接近的由矢径r_i^∗+δr_i确定的位置，称为等时变分。在等时变分中我们不考察系统的运动过程，而是比较系统在给定时刻约束允许的无限接近的位置（构形）。

虚位移定义为质点系在同一时刻、同一位置两组可能位移之差，即δr_i=dr_i^（1）-dr_i^（2）（i=1，2，…，n），或δx_i=dx_i^（1）-dx_i^（2）（i=1，2，…，3n）。

现在我们研究两个在相同时间dt内的可能位移。根据式（17-6），有

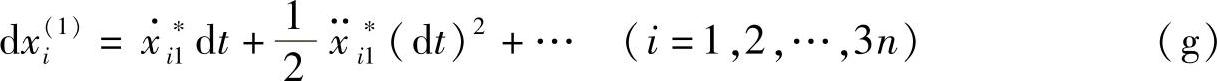
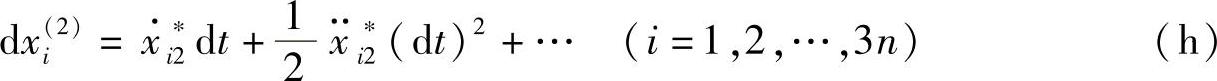
可能速度v_ij^∗和可能加速度a_ij^∗（j=1，2）满足式（17-2）～式（17-5）。将两组可能位移相减，得

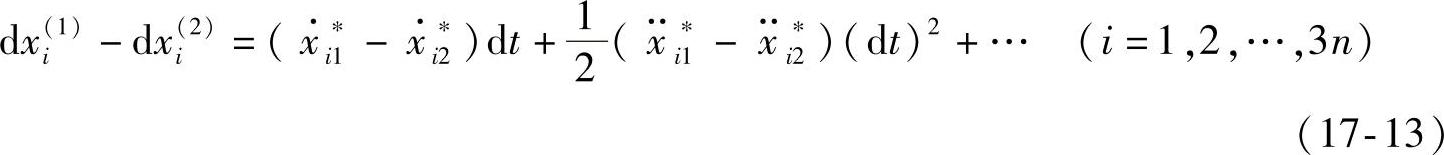
（1）若尔当变分

先将t=t^∗，r_i=r_i^∗，v_i=v^∗_i1代入方程（17-3）并在两边同时乘以dt，然后将t=t^∗，r_i=r_i^∗，v_i=v_i2^∗代入方程（17-3）并在两边同时乘以dt，最后将得到的两个方程相减，得

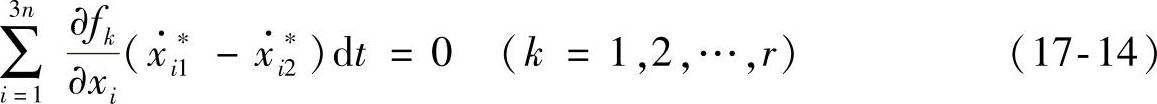
类似地，由方程（17-2）可得

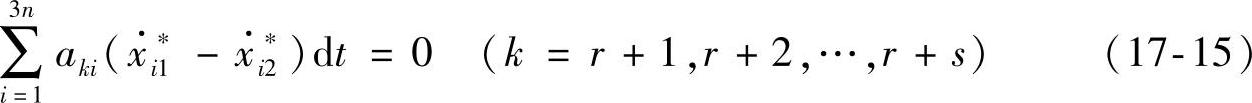
如果δv_i=v^∗_i1-v^∗_i2≠0，则式（17-13）中的主要部分是dt的线性项，即δv_idt，并且根据式（17-14）和式（17-15）知，它满足方程组（17-9）和方程组（17-10），即虚位移δr_i的分量是

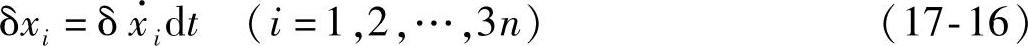
在v^∗_i1≠v_i2^∗的假设下，这个等时变分称为若尔当变分。

（2）高斯变分

利用相同的过程处理式（17-4）和式（17-5）（只是要代入a_i=a_ij^∗（j=1，2），乘以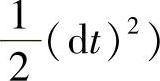，可以得到

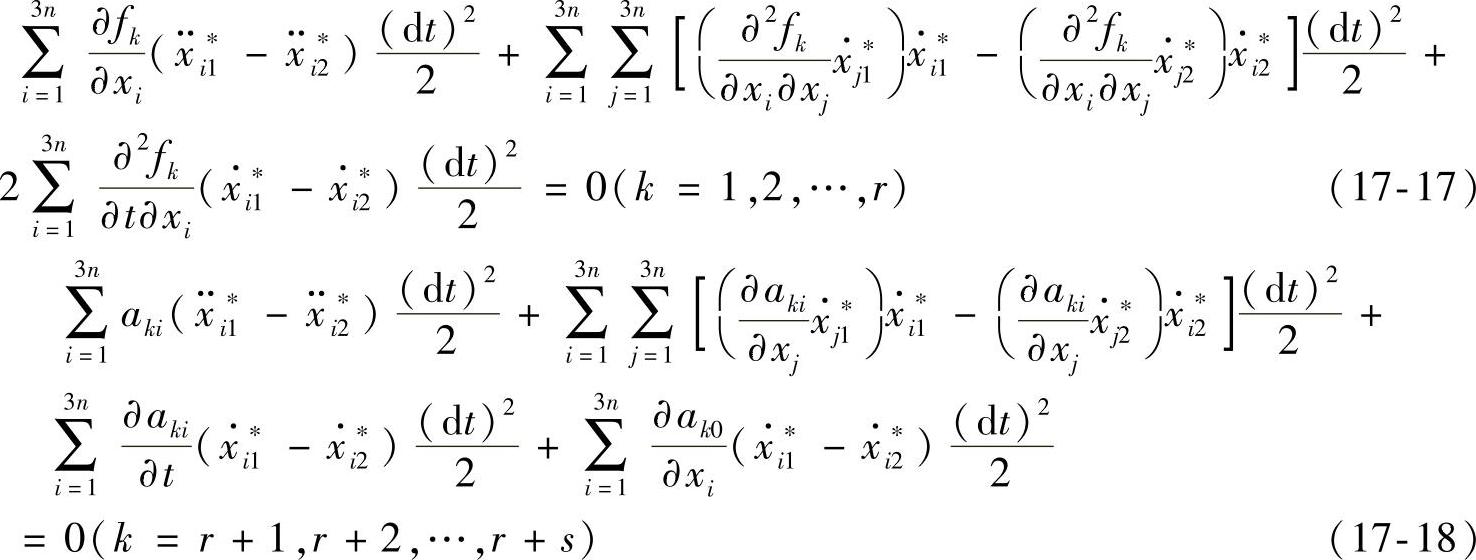
如果v^∗_i1=v^∗_i2，但δa_i=a^∗_i1-a^∗_i2≠0，则式（17-13）中的主要部分等于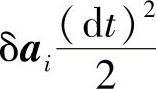。当v^∗_i1=v^∗_i2时，式（17-17）和式（17-18）除了第1项以外的所有求和项都等于零。根据式（17-17）和式（17-18）知，它满足方程组（17-9）和方程组（17-10），即虚位移δr_i的分量是

在v^∗_i1=v_i2^∗，但a^∗_i1≠a_i2^∗的假设下，这个等时变分称为高斯变分。