我们来研究质点系P_i（i=1，2，…，n）相对于固定笛卡儿坐标系的运动，系统的状态由系统内点的矢径r_i和速度v_i确定。系统运动时其各点的位置和速度经常不能是任意的，对矢径r_i和速度v_i的限制不因受力而改变，称为约束。如果系统不受约束，则系统称为自由的。当存在一个或多个约束时，系统称为非自由的。

例1 质点可以沿着过坐标原点给定的平面运动。如果笛卡儿坐标系统的Oz轴垂直于该平面，则z=0是约束方程。

例2 质点沿着以原点为中心、半径为R=f（t）的球面运动。如果x，y，z是运动点的坐标，则约束方程为x²+y²+z²-f²（t）=0。

例3 两个质点P₁和P₂用长为l的不可伸长的绳相连，约束用关系式l²-[（x₂-x₁）²+（y₂-y₁）²+（z₂-z₁）²]≥0给出。

例4 质点在空间中运动并保持在第一象限内或边界上，约束用不等式x≥0，y≥0，z≥0给出。

例5 （冰刀的运动）设冰刀沿着水平冰面运动。冰刀以细杆为模型，在运动过程中杆上一点C（图17-1）的速度始终沿着杆。如果Oz轴竖直向上，x，y，z是C的坐标，而φ是杆与Ox轴的夹角，则约束由两个方程z=0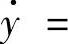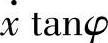，给出。

例6 （纯滚动的圆柱）半径为R的圆柱作纯滚动，如图17-2所示。圆柱有约束z_O=R，，其中φ为圆柱的转角。

图17-1 冰刀的运动

图17-2 纯滚动的圆柱

例7 有质量的质点在有势力F=F（x，y）作用下，在平面xOy上运动，所受约束可用方程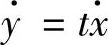表示。

1.双向约束与单向约束

一般情况下约束用关系式

（k=1，2，…，r+s） （a）给出。等式约束方程对应的约束称为双向约束，或双侧约束（图17-3a）。在上面的例1、例2、例5、例6和例7中，约束是双向的。这里r+s表示双向约束数。

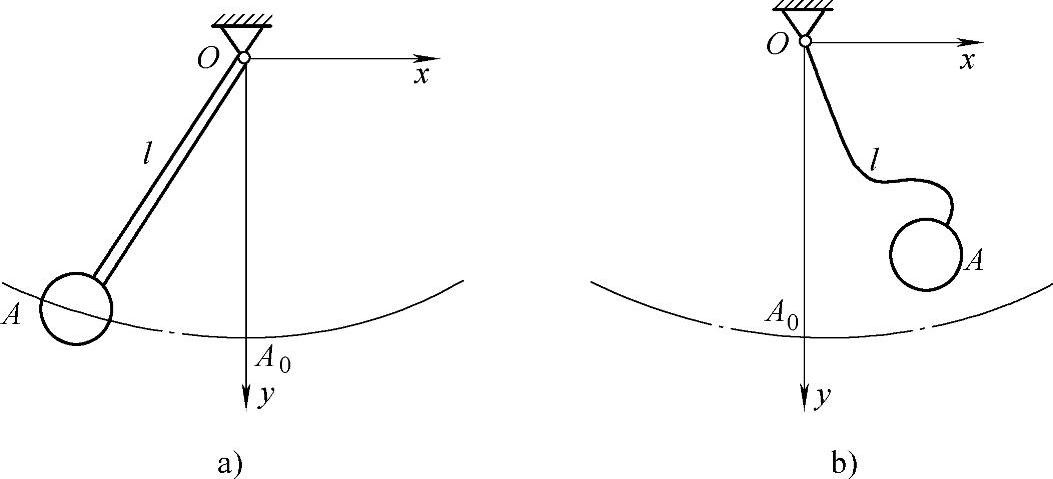
图17-3 单摆

a）双向约束 b）单向约束

如果约束关系出现不等号形式时，即 （k=1，2，…，R） （b）此不等式约束方程对应的约束称为单向约束，或单侧约束（图17-3b）。在上面的例3、例4中，约束是单向的。这里R表示总约束数。下面我们不再研究有单向约束的系统。

2.位形空间和位置约束

在第11章中曾将系统内各质点的3n个坐标的集合，定义为质点系的位形。建立抽象的3n维正交欧氏空间（x₁，x₂，…，x_3n），称为质点系的位形空间。质点系在每个瞬时的位形，与位形空间中的抽象点一一对应。随着时间的变化，位形空间中点的位置亦随之改变而描绘出一条超曲线。对各质点的空间位置所加的限制称为位置约束。设系统内共有r₁（r₁≤r）个位置约束方程，写作

f_k（x₁，x₂，…，x_3n；t）=0 （k=1，2，…，r） （c）此约束方程对应于位形空间中的超曲面，称为约束曲面。上面的例1、例2是位置约束。

单个质点是n=1的特殊质点系，所对应的位形空间就是实际三维空间，约束曲面是三维空间中的实际曲面，约束的作用是迫使实际质点沿实际的约束曲面运动。对于n>2的一般质点系，上述位形空间和约束曲面都是抽象概念。必须注意，位形空间中的抽象与三维空间中的实际质点，是截然不同的两种概念。

3.状态空间和运动约束

运动中的质点在任一瞬时所占据的位置及所具有的速度合起来称为质点在该瞬时的运动状态。采用直角坐标系时，质点的运动状态由六个标量x₁（t），x₂（t），x₃（t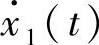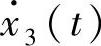），，，完全确定，称为状态变量。建立抽象的六维正交欧氏空间（x₁，x₂，x₃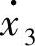，，，），称为质点的状态空间，或相空间，则质点在每个瞬时的运动状态与状态空间中的点一一对应，后者称为相点。随着时间的推移，相点在相空间中位置亦随之改变，所描绘出的超曲线称为质点运动的相轨迹。应注意状态空间与实际空间、相点与实际质点、相轨迹与实际运动轨迹是根本不同的两种概念。实际空间中的运动轨迹只能表示质点空间位置的变化，而状态空间中的相轨迹则能给出质点的空间位置和速度变化过程的全貌。

对于由n个质点P_i（i=1，2，…，n）组成的质点系，系统内各质点的坐标和速度共6n维空间（x₁，x₂，…，x_3n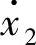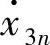；，，…，），称为质点系的状态空间。状态空间不同于位形空间，后者可看做前者的3n维子空间，它只能反映系统内各质点的位置变化而不能反映各质点的速度变化，而状态空间则能使我们有可能从几何观点出发研究质点系运动过程的全貌。

仅对速度所加的限制称为速度约束。不仅对位置而且对速度所加的限制称为运动约束，对应的约束方程为f_k（x₁，x₂，…，x_3n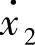；，，…，；t）=0 （k=1，2，…，r+s） （d）上面的例5、例6和例7是运动约束。(www.daowen.com)

4.几何约束、微分约束

约束方程中只含力学系统中质点坐标和时间的约束称为几何约束，对应的约束方程为

f_k（x₁，x₂，…，x_3n；t）=0 （k=1，2，…，r） （17-1）

几何约束包括位置约束和可用几何约束形式表示的运动约束。

约束方程中不仅包含质点坐标、时间，而且包含速度的约束称为微分约束。微分约束包括可积微分约束和不可积微分约束。可积微分约束可以转变为几何约束。

位置约束是力学概念，几何约束是数学概念。位置约束属∙于∙几何约束，如例1；但反过来不成立，几何约束不一定是位置约束，还包括可积分的运动约束，如例6中约束可写成s=Rφ。

运动约束是力学概念，微分约束是数学概念。运动约束不一定是微分约束，运动约束也可以采用几何约束形式表示，如例6；反过来微分约束也不∙一∙定∙是运动约束，用几何约束表示的位置约束求导后可以变成微分约束。我们假设相应的不可积微分约束对于速度分量，，是线性的，则

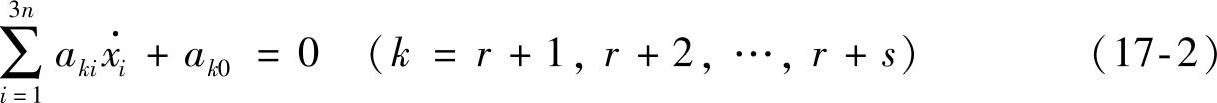
式中，系数a_ki，a_k0均为x_i（i=1，2，…，3n）和t的函数。特殊情况下r和s₁可以等于零。若a_k0=0，则称为关于速度v_i是齐次的约束；反之，关于速度v_i是非齐次的约束。

几何约束和不可积一阶线性微分形式的双向约束称为普发夫（Pfaff）约束。我们把不可积的一阶线性微分约束数用s₁（s₁≤s）表示。我们只讨论普发夫约束系统。

5.定常系统和非定常系统

若约束方程中不显含时间t，则它称为定常约束；反之称为非定常约束。如果系统是自由的或者只有定常约束，则称为定常系统。如果系统的约束中至少有一个是非定常的，则称为非定常系统。

例1、例3、例4、例5和例6是定常系统；例2和例7是非定常系统。

6.完整系统和非完整系统

如果质点系的所有约束可以用几何约束形式表示的系统，则称为完整系统。如果质点系的约束中含有不可积的微分约束的系统，则称为是非完整系统。

双向位置约束数用r₁表示，可积的微分约束数用r₂表示，双向完整系统约束数用r表示，且r=r₁+r₂；双向非完整系统约束数用s表示。

例1和例2是几何约束所以是完整系统。例6是微分约束可以积分成为x_O=Rφ+C，因此是完整系统。例5和例7是不可积的微分约束，属于非完整系统。

注释1 例5中的微分约束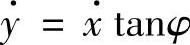是不可积的，下面给出证明。假设不然，即x，y，φ满足关系式f（x，y，φ，t）=0，设x，y，φ相对于冰刀的真实运动，求f对时间的全导数，即

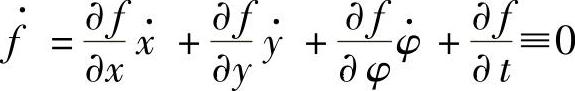
利用约束方程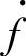，可以写成为

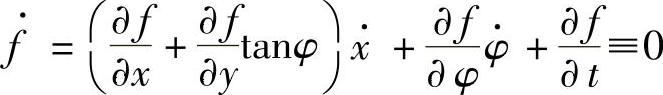
由于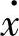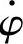，是独立的，故

再根据角度φ的任意性，函数f对其所有变量的偏导数都等于零，即f不依赖于x，y，φ，t，因此，假设约束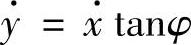可积是不正确的。

注释2 例1和例6中的系统是完整定常的；例2中的系统是完整非定常的；例5中的系统是非完整定常的。例7中的系统是非完整非定常的。