在日常生活和工程实际中，有大量绕定轴转动的刚体（电动机、柴油机、电风扇、车床主轴等），如何使这些机械在转动时不产生破坏、振动与噪声，是工程师应当关心的问题。如果这些机械在转动起来之后轴承受力与不转动时轴承受力一样，则这些机械一般不会产生破坏，也不会产生振动与噪声。我们可以把约束力分成静约束力与动约束力，静约束力是刚体静止时受到的约束力；动约束力是由于惯性力引起的约束力。对绕定轴转动的刚体，如果能够消除轴承动约束力，使轴承只受到静约束力作用，就可以做到这一点。为此，先把任意一个绕定轴转动刚体的轴承全约束力（包括静约束力与动约束力）求出来，然后再推导出消除动约束力的条件。

设任一刚体绕轴AB作定轴转动，角速度为ω，角加速度为α，取此刚体为研究对象，转轴上一点O为简化中心，其上所有的主动力向O点简化的主矢与主矩以R和M_O表示，惯性力系向O点简化的主矢与主矩以R_I和M_IO表示（注意R_I没有沿z轴方向的分量），轴承A，B处的五个全约束力分别以F_Ax，F_Ay，F_Bx，F_By，F_Bz表示，均如图16-5所示。

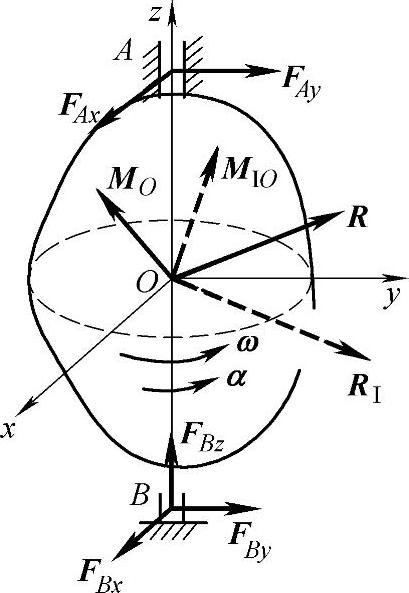
图 16-5

为求出轴承A，B处的全约束力，建立坐标系如图16-5所示，根据 质点系的动静法。这形成一个空间任意平衡力系，列平衡方程如下：

∑F_x=0，F_Ax+F_Bx+R_x+R_Ix=0 （a1）

∑F_y=0，F_Ay+F_By+R_y+R_Iy=0 （a2）

∑F_z=0，F_Bz+R_z=0 （a3）

∑M_x=0，F_By·OB-F_Ay·OA+M_x+M_Ix=0 （a4）

∑M_y=0，F_Ax·OA-F_Bx·OB+M_y+M_Iy=0 （a5）

由上述5个方程解得轴承全约束力为

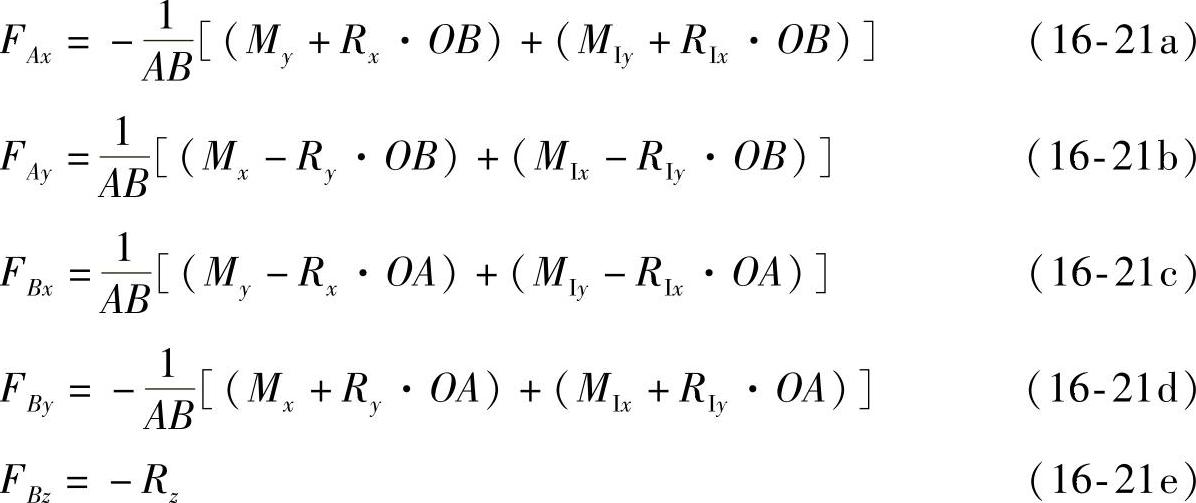(www.daowen.com)

由于惯性力没有沿z轴方向的分量，所以推力轴承B沿z轴方向的约束力F_Bz与惯性力无关，而与z轴垂直的轴承约束力F_Ax，F_Ay，F_Bx，F_By显然与惯性力系的主矢R_I和主矩M_IO有关。由于R_I，M_IO引起的轴承约束力称为动约束力，要使动约束力等于零，必须有

F_Ix=0，F_Iy=0，M_Ix=0，M_Iy=0 （b）即要使轴承动约束力等于零的条件是：惯性力系的主矢等于零，惯性力系对于x轴和y轴的主矩等于零。

由式（16-7）和式（16-13），应有

ma_Cx=0，ma_Cy=0，J_xzα-J_yzω²=0，J_yzα+J_xzω²=0 （c）

由此可见，要使惯性力系的主矢等于零，必须有a_C=0，即转轴必须通过质心。而要使M_Ix=0，M_Iy=0，必须有J_xz=0，J_yz=0，即刚体对于转轴z的惯性积必须等于零。

于是得结论，刚体绕定轴转动时，避免出现轴承动约束力的条件是：转轴通过质心，刚体对转轴的惯性积等于零。

如果刚体对于通过某点的z轴的惯性积J_xz和J_yz等于零，则称此轴为过该点的惯性主轴。通过质心的惯性主轴，称为中心惯性主轴。所以上述结论也可叙述为：避免出现轴承动约束力的条件是，刚体的转轴应是刚体的中心惯性主轴。

设刚体的转轴通过质心，且刚体除重力外，没有受到其他主动力作用，则刚体可以在任意位置静止不动，称这种现象为静平衡。当刚体的转轴通过质心且为惯性主轴时，刚体转动时不出现轴承动约束力，称这种现象为动平衡。能够静平衡的定轴转动刚体不一定能够实现动平衡，但能够动平衡的定轴转动刚体肯定能够实现静平衡。

事实上，由于材料的不均匀或制造、安装误差等原因，都可能使定轴转动刚体的转轴偏离中心惯性主轴。为了避免出现轴承动约束力，确保机器运行安全可靠，在有条件的地方，可在专门的静平衡与动平衡试验机上进行静、动平衡试验，根据试验数据，在刚体的适当位置附加或去掉一些质量，使其达到静、动平衡。静平衡试验机可以调整质心在转轴上或尽可能地在转轴上；动平衡试验机可以调整对转轴的惯性积，使其对转轴的惯性积为零或尽可能地为零。

当然，在工程中也有相反的实例，即制造定轴转动刚体时，故意制造出偏心距，如某些打夯机，正是利用偏心块的运动来夯实地基的。