设质点系由n个质点P_i（i=1，2，…，n）组成，每个质点在运动过程中形成的达朗贝尔惯性力组成一空间惯性力系（F_I1，F_I2，…，F_In），其中

F_Ii=-m_ia_i （i=1，2，…，n） （a）

利用第4章中叙述的力系简化方法，可将此惯性力系向空间中任意选定的简化中心O简化，化作在点O上作用的主矢R_I和主矩M_IO：

（F_I1，F_I2，…，F_In）⇔（R_I，M_IO） （b）

其中

同一惯性力系向不同的简化中心简化，其主矢的大小和方向保持不变，而主矩则随简化中心的不同而改变。若A为另一简化中心，则不同简化中心的主矩之间有与式（4-11）相同的关系式：

M_IA=M_IO+r×R_I （16-6）

式中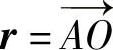，为A至O的矢径。(www.daowen.com)

设简化中心A为空间中任意动点，点A相对固定点O的矢径为r_A，质点相对点O和点A的矢径分别为r_i和ρ_i，则有

r_i=r_A+ρ_i （c）

设v_i=dr_i/dt，a_i=d²r_i/dt²分别为质点P_i的速度和加速度，将质点P_i的达朗贝尔惯性力F_Ii=-m_ia_i代入式（16-5），展开后可将惯性力系的主矢和主矩化作

即

R_I=-ma_C （16-7）

即

式中，p和L_A分别为质点系的动量和对动点A的动量矩；v_A为点A的速度。式（16-7）和式（16-8）表明，惯性力系的主矢R_I等于质点系全部质量集中在质心C处的达朗贝尔惯性力，主矩M_IA等于质点系对点A的动量矩对时间的导数以及点A的速度与质点系动量的矢量积之和的负值。对于简化中心为固定点O和质心C的特殊情形，主矩M_IO和M_IC分别简化为