（一）基本理论

在进行农田水利田间工程规划，排水沟道（以排地下水为主）设计、估计河道侧渗影响以及地下水开发利用规划等时，除了需要摸清计算地段水文地质构造外，还要准确掌握水文地质参数的数值。有些参数（如水力传导度K，给水度μ）虽然可以通过在田间钻探取样然后进行室内测定，但天然情况下的水文地质条件十分复杂。试图通过少数的钻孔取样资料求得的参数来代表大面积的情况，往往是不可靠的，这样就发展了野外实地测定的方法。

利用野外实测的地下水动态资料求参数的实质多是分析某一外部因素（如河沟水位变动、水井抽水、降雨入渗，地下蒸发等）影响下的地下水运动，测定外部因素在量上的数值及相应时期的地下水动态，利用解析解方法或数值计算方法反求参数（数学上称这种运算为逆运算）。这些外部因素可以是天然状况下的 （如降雨、蒸发等），也可以是人为的（如抽水试验、人工灌溉等）。在农田水利中最常用的一种方法是通过在河沟水位变化期间测定河沟附近地下水动态资料反求参数。

本试验的目的是希望在实验室内模拟野外的条件下 （经过一定简化），试验者通过有关试验数据的观测及资料分析工作，掌握进行野外实际试验的一般规律、观测孔的布置、资料的取得以及反求参数的分析计算方法。此外，室内模型（用砂槽）试验还有助于探索一定边界条件下地下水运动的机理，并可对某些理论研究成果进行验证。

设有一沟间地段，降雨入渗强度为ε，土层的孔隙率为μ，在无排水设施情况下，经过t时间后，地下水位的上升高度为εt/μ。在降雨入渗强度很小，而入渗时间又较短时，除排水沟邻近地段，由于有排水沟的控制，地下水上升高度小于εt/μ外，其余大部分地段应与无排水设施情况一样 （即水位上升高度为εt/μ）。这种情况下雨停后的排水过程，可以近似地按沟水位与地下水位齐平，在某一时刻沟水位突然下降一个深度的情况 （图1-1-6）。

地下水运动基本方程以及定解条件为

初始条件及边界条件为

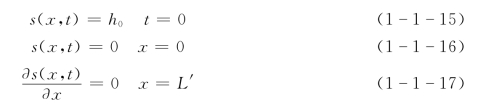
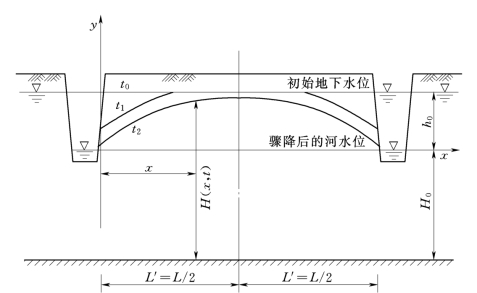
图1-1-6　排水沟水位突然下降一个深度的情况

令s′=s-h0

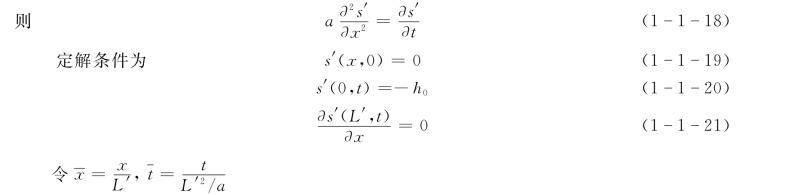
得

初始条件及边界条件为

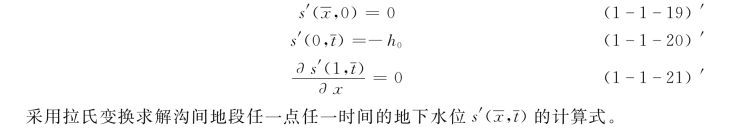
式 （1-1-22）经拉普拉斯（LaplaceTransformation）变换后，得

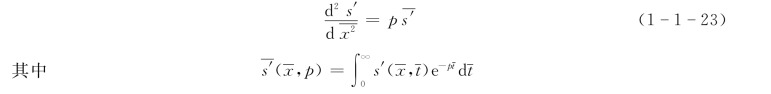
式 （1-1-23）的通解为

式 （1-1-20）′、式 （1-1-21）′经拉普拉斯变换后，得

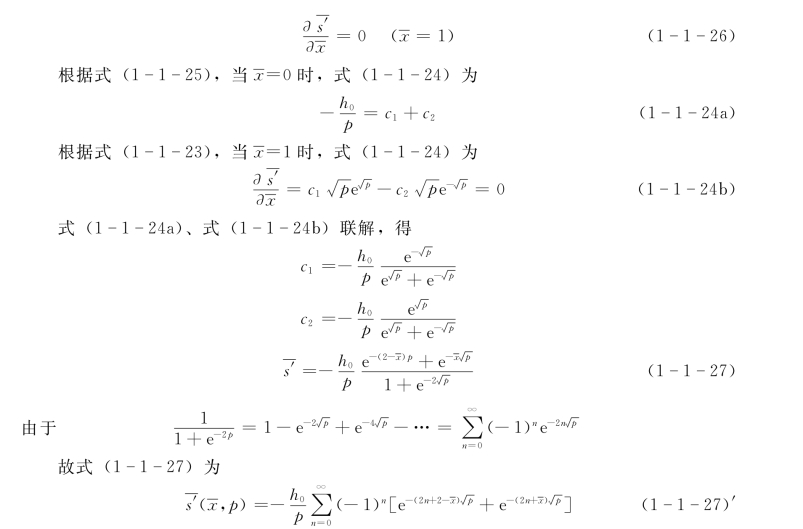
查拉普拉斯逆变换表知

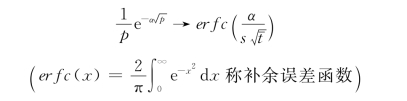
所以

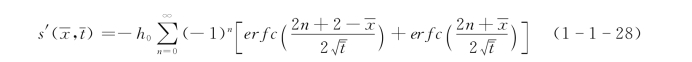
式 （1-1-28）为误差函数形式的解，写为双曲函数的形式得

根据拉普拉斯变换的分解定理

F1（P）、F2（P）为包含P的多项式的函数，且F2（P）不包含常数项，Pn为F2之根。

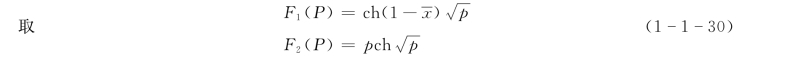
求F2（P）的根

有了地下水位的计算式，从一侧流向河沟的排水流量计算公式即可推出。根据

(www.daowen.com)

从式（1-1-42）可求得一侧排水流量计算公式为

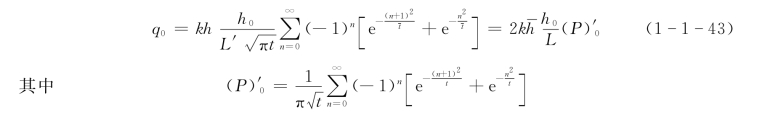
从式（1-1-43）可求得另一种形式

当t＞0.3时，式 （1-1-43）′可简化为

在Excel中，绘制lgt—lgsc关系曲线，在理论上应呈一直线。因此，如果在野外或室内模型能重现上述初始条件和边界条件的情况下，测得不同时刻t及河间地段中间断面处的水位，即可用图解分析法求得压力传导系数a值。

对式（1-1-42）取对数并整理，得

式 （1-1-46）表示，排向一侧河沟的流量q0与时间之间呈指数关系。在Excel中点绘t—lgsc关系，在理论上应呈一条直线，且斜率应与t—lgsc的斜率一致，因此从t—lgq0线的截距即可求得给水位度μ值。

（二）试验装置

本试验是在净空为400mm×100mm×55cm的钢结构玻璃砂槽内进行的。试样是经过筛选洗净的细砂，按一定的容重均匀装填并逐渐由下而上充水饱和。排水沟为一完整沟，由聚氯乙烯条板焊接的透水隔栅分隔而成。为测定地下潜水面高程，在砂槽的一定距离上装设观测井。观测井为内径2cm的塑料花管，外包铜丝滤网，穿透整个砂层。排水沟的水位及出流量的量测由软管接一平水漏斗控制，试验装置的结构及相关尺寸如图1-1-7所示。另需配备秒表两只，50mL、100mL及500mL量筒各一个。

（三）试验方法及步骤

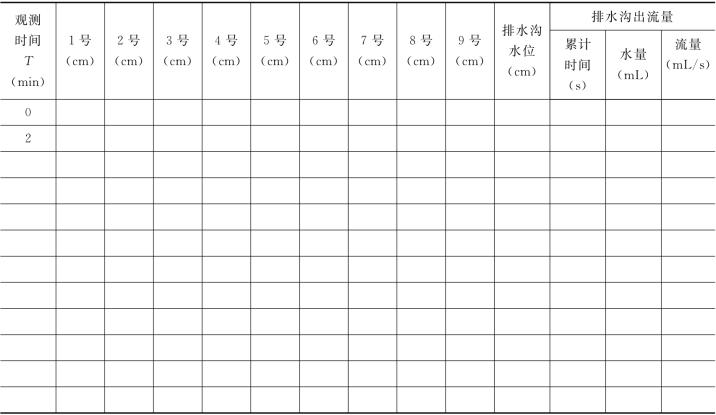
本试验是测定在排水沟的作用下地下水运动的不稳定过程，因此试验开始前必须做好一切准备工作（找准观测井位，进行测压管排气等）。试验开始前，应使原始地下水位与河沟水位一致（即地下水处于静止状态），并记下各观测井及排水沟原始水位 （作为0时段），试验开始（计时开始），打开排水沟出水管阀门，将排水沟水位瞬时下降一个深度（若排水沟容积太大，水不易瞬时排出时，可采取辅助方法排水），按记录表所规定的时刻（或自定时刻）记录各观测井的水位及排水沟的出流量，流量的测量方法采用体积法。试验记录格式见表1-1-5。

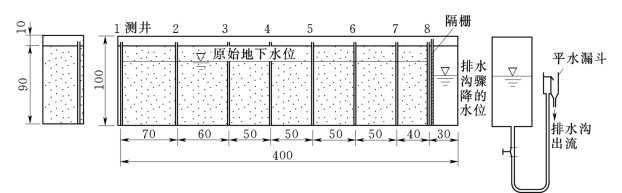
图1-1-7　试验装置的结构图及有关尺寸 （单位：cm）

表1-1-5　排水沟骤降试验记录表

（四）试验成果分析

1.压力传导系数a值的分析推断

（1）1号观测井观测资料整理，见表1-1-6。

表1-1-6　1号观测井观测资料整理

表1-1-6中，sc=Hc-H0，Hc为1号测井水位读数，H0为排水沟瞬降后的水位。

（2）在Excel中点绘t—lgsc关系，通过多数点据，绘制直线，该直线斜率为J

J值亦可通过作图求得，如图1-1-8所示，即

将上式代入式（1-1-47），可求得a值。

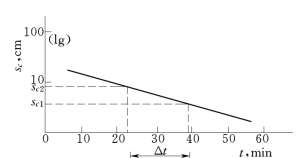
图1-1-8　J值计算图

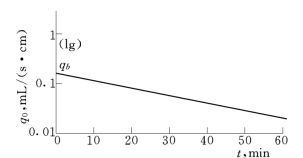
图1-1-9　直线与纵轴截距

2.给水度μ值的分析推断

在Excel中点绘t～lgq0关系，通过多数点据，绘制直线，该直线与纵轴截距为lgqb，见式（1-1-48）及图1-1-9。

由于a值已在前面步骤求得，故μ值可通过式（1-1-48）求得。