1.幂指数（Power Law）

对于幂指数模型，粘度的表达式如下

式中，μ₀为名义粘度；K为一致性指标；；D₀为D的临界值；n为幂率指数；I₂为第二应变率张量不变量=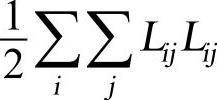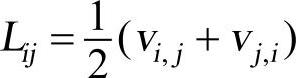，；v_ij为在第j方向上的第i方向速度梯度。

这种关系被用于模拟的聚合物、血液、橡胶求解。K的单位取决于n的值。

2.Carreau模型

对于Carreau模型，粘度的表达式如下

其中：μ∞—无限剪切率时的粘度；μ₀—剪切率为0时的粘度；λ—时间常数；n—幂指数。

通常情况下，流体的粘度行为就像一个幂律模型的剪切率对于中间值，而其余的有界零/无限剪切速率。

该模型移除了一些与幂率模型相关的不足。该流体的粘度被假定为具有下限和上限。

3.Bingham模型(www.daowen.com)

Bingham模型：对于“ideal”Bingham模型，粘度的表达式

式中，μ₀为塑性粘度；G为屈服强度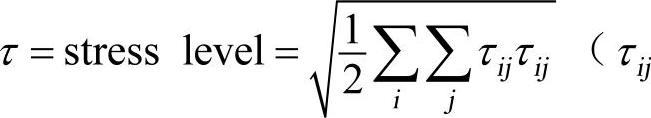；为第i面第j方向上的额外压力）。

如图6-7所示，只要应力小于屈服应力，则流体行为为刚性。当应力超过了屈服强度，则增加的应力与应变率成比例，这种行为与牛顿流体相同。但这种模型进行数值计算是很困难，因此实际使用是的模型为双线性Bingham模型。

式中，μ_r为牛顿粘度。

图6-8所示为双线性Bingham模型中的应力—应变率关系。μ_r至少要比μ₀大一个数量级。典型情况下，μ_r^一般的取值为100倍的μ₀以便模拟真实的Bingham流体行为。

图6-7 理想Bingham模型中的应力—应变率关系

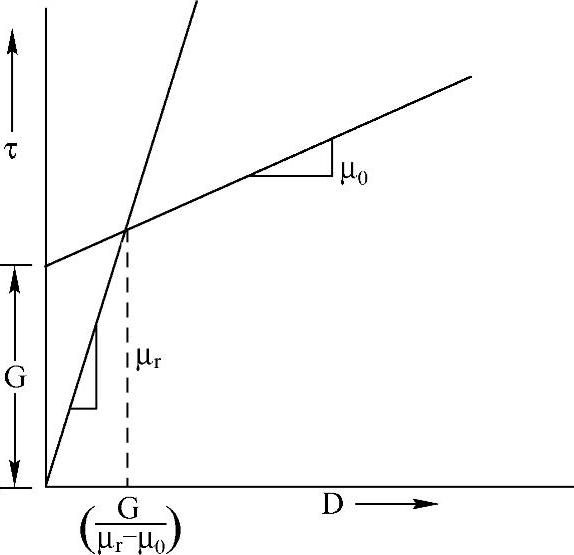
图6-8 双线性Bingham模型中的应力—应变率惯性