对于流体，当惯性效应大于粘性效应时，则流体的状态可能就为湍流。用户负责确定流体的状态是层流还是湍流。湍流流动模型很多，但大致可以归纳为以下三类：第一类是湍流输运系数模型；第二类是抛弃了湍流输运系数的概念，直接建立湍流应力和其他二阶关联量的输运方程；第三类是大涡模拟。前两类是以湍流的统计结构为基础，对所有涡旋进行统计平均。大涡模拟把湍流分成大尺度湍流和小尺度湍流，通过求解三维经过修正的Navier-Stokes方程，得到大涡旋的运动特性，而对小涡旋运动还采用上述的模型。实际求解中，选用什么模型要根据具体问题的特点来决定。选择的一般原则是精度要高、应用简单、节省计算时间，同时也具有通用性。

FLOTRAN采用了湍流输运系数模型。当流体的状态为湍流时，则流体中的每一个点都是波动变化的。因此，湍流速度的表达式由常时均值速度和波动速度组成，即

式中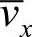，为x方向的常时均值速度；v_x′为x方向的波动速度。

将湍流速度代入到N-S方程中，该方程将被时间进行平均。湍流速度中波动速度的平均值为0，湍流速度的平均值为平均速度。在计算速度的平均值时，积分时间间隔是任意选择的，但要保证真实时间的瞬态效应不影响积分中的时间。下式给出了波动速度平均值和湍流瞬时速度的平均值表达式：

式中，δ_t为波动周期。将（2-19）代入到动量方程中，使用时间进行平均，则会导致出现附加项。动力方程中的速度是平均值，所以在随后的表达式中使用平均速度进行表示。附加项如下

式中，σ^R为雷诺应力。(www.daowen.com)

湍流输运系数模型假设速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。即

有效粘度是层流粘度（层流粘度是流体的属性）和湍流粘度（湍流粘度从湍流模型中计算所得）之和。即

μ_e=μ+μ_t （2-24）

如果密度是变化的流动过程，如燃烧问题，我们可以用法夫雷（Favre）平均。这样才可以求解存在密度变化的流动问题。法夫雷平均就是除了压力和密度本身以外，所有变量都用密度加权平均。变量的密度加权平均定义为

波浪线表示的Favre平均变量。