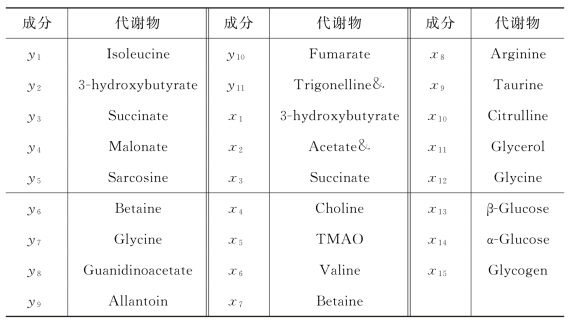
上节探讨的PLS回归模型被应用到代谢组学数据集中,其中控制组有6只老鼠,慢性萎缩性胃炎组有6只老鼠,分别收集尿液样本和血液样本[112]。这个数据集包括12只老鼠的11个尿液代谢物成分和15个血液代谢物成分。本节的目标是分析尿液代谢物成分y＝(y 1,y 2,…,y 11)T和血液代谢物成分x＝(x 1,x 2,…,x 15)T之间的关系。表6.3.1给出了成分y 1,y 2,…,y 11,x 1,x 2,…,x 15对应的代谢物名称。

表6.3.1　尿液代谢物成分结构y＝(y 1,y 2,…,y 11)T和血液代谢物成分结构x＝(x 1,x 2,…,x 15)T

因为样本观测值的个数小于成分解释变量的部分数,使用PLS回归分析来分析成分变量y和x之间的关系,记y和x的样本数据集分别为Y和X,计算y和x的样本中心

则中心化的成分变量为y⊖对应的数据集为Y⊖的clr系数为v＝(v 1,v 2,…,v 11)T和u＝(u 1,u 2,…,u 15)T,则对应的数据集分别为V＝clr(Y⊖

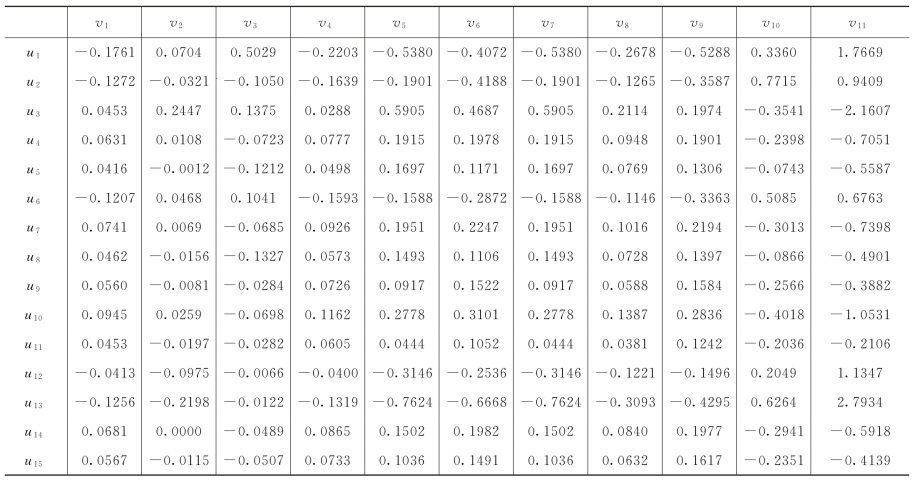
为了建立V和U的PLS回归模型,首先需要计算PLS成分的个数。在这个例子中,使用留一交叉验证法。表6.3.2给出了在不同的成分个数下对因变量v 1,v 2,…,v 11的预测的均方根误差(RMSEP),其中“CV”是RMSEP的交叉验证估计,“adjCV”是RMSEP偏差修正后的交叉验证估计。通过计算,最优成分个数是3个,在3个PLS成分个数下,因变量v 1,v 2,…,v 11的RMSEP达到最小值。确定了PLS成分的个数后,就可以得到V和U的关系,即,其中估计的回归系数矩阵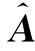是一个11×15矩阵(见表6.3.3)。表6.3.3中每一列代表了对应的因变量v j(j＝1,2,…,11)和自变量u 1,u 2,…,u 15的回归系数,即它是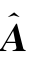中对应的行。可以证明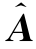的每行求和为零,的每列求和也为零。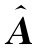的回归系数可以使用jackknife方法进行检验,可以通过R软件的程序包pls中的函数jack.test来实现。黑色字体的值代表了参数在0.1的显著性水平下是显著的。

表6.3.2　不同成分个数下使用留一交叉验证法的预测的均方根误差(RMSEP)(www.daowen.com)

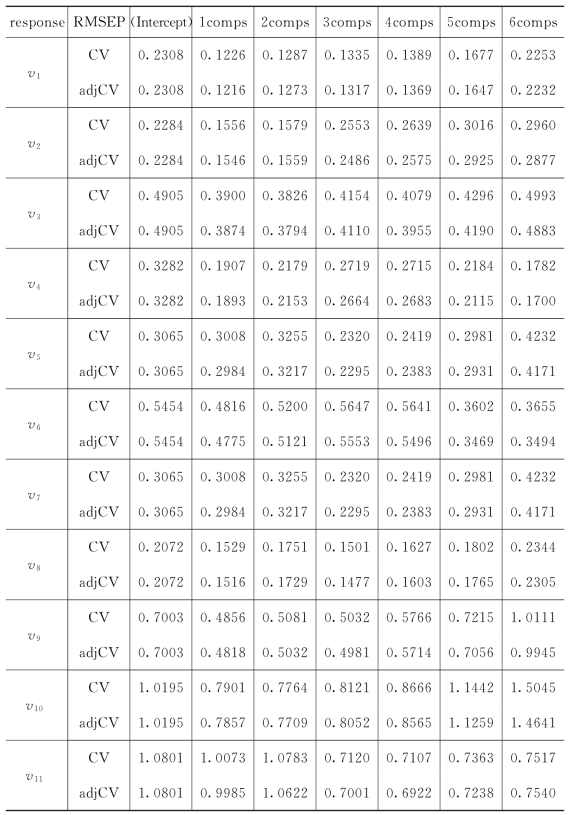
表6.3.3　clr数据集V和U的估计的回归系数矩阵

通过定理6.2.4,回归系数矩阵也是成分变量y⊖的系数,因此最终预测的成分数据集为

根据表6.3.3中的结果,回归系数矩阵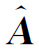的解释如下:valine(x 6)的相对信息对解释isoleucine(y 1)的相对信息有显著影响,因为这两个代谢物有相同的valine,leucine和isoleucine生物路径;sarcosine(y 5)和glycine(y 7)有相同的回归系数,即A^的第五行和第七行是相同的,这与两个代谢物位于glycine,serine和threonine代谢的上游和下游的事实一致;citrulline(x 10)的相对信息对解释guanidinoacetate(y 8)的相对信息有显著影响,这可能是由于相同的arginine和proline代谢途径;acetate(x 2)的相对信息对解释allantoin(y 9)的相对信息和trigonelline(y 11)的相对信息有显著影响,这可能是因为这三种代谢物参与了肠道菌群代谢。这些参数的解释与生物学意义一致。为了评价提出模型的拟合效果,计算出模型R 2为0.6601,这意味着提出的模型有高的精度。而且,单形上建立PLS回归模型的可能性保证了参数解释不必通过上面的clr系数来确定,基于矩阵乘积运算能直接考虑原始成分部分。