为了建立单形上的PLS回归,首先需要给出单形上的PLS因子。在单形上,成分变量的PLS因子是加权成分变量的扰动。因为不同成分变量的部分数是不相同的,可以使用矩阵乘积运算A x,其中A代表权重矩阵。为了进行扰动运算,每个成分变量权重矩阵的行数必须相同。

根据性质2.3.2(3),成分因变量y 1,y 2,…,y p和成分自变量x 1,x 2,…,x q的PLS因子分别为t 1,t 2,…,t r和s 1,s 2,…,s rl＝1,2,…,rx,l＝1,2,…,r其中y＝矩阵F l和R l分别记为F l＝(F l 1,F l 2,…,F lp)和R l＝(R l 1,R l 2,…,R lq),其中F lj,R lk(j＝1,2,…,p;k＝1,2,…,q)是权重矩阵。假定PLS因子t l和s l有d(d≥2)个成分,则F lj是一个d×C j矩阵,R lk是一个d×D k矩阵,而且它们满足F lj 1Cj＝0d,0d,根据性质2.4.4,t l的样本中心为

其中第三个等式成立是因为F lj 1Cj＝0d。类似地,s l的样本中心为n d。记PLS因子t l和s l的样本数据集分别为

根据公式(2.3.3)可以得到

基于成分变量样本协方差的定义,从公式(2.4.4),(2.4.5)和(6.2.1)可以得到解PLS因子t l和s l的样本协方差为

类似于6.1节,使用SIMPLS算法,考虑优化问题

定理6.2.1　对于优化问题(6.2.2),存在一个解R l＝F l＝(l＝1,2,…,r),其中k＝(k 1,k 2,…,k d)T是一个任意的实数向量且满足k T k＝1,k T 1d＝0(w l,θl的定义见定理6.1.1)。

证明　首先解决如下的优化问题:

假定优化问题(6.2.3)前l－1个解矩阵为R 1,R 2,…,R l－1。使用拉格朗日乘数法,目标函数是

通过最大化目标函数J l(R,F)可以得到解R l,F l。将目标函数分别关于R,F求偏导,得到的正规方程为

如果公式(6.2.4),(6.2.5)两边分别右乘R T,F T,而且取迹,可得

则目标为最大化2λ。公式(6.2.4)两边分别右乘矩阵UU T R T k(k＝1,2,…,l－1)且取迹,由于tr(RUU T)＝0,可以得到

使用公式(6.2.6)来简化(6.2.4)得到

(1)当l＝1时,公式(6.2.8)为RUV T VU T＝(2λ)2R。根据定理6.1.1,w 1是矩阵UV T VU T最大特征值对应的单位特征向量,则R 1＝其中k＝(k 1,k 2,…,k d)T是一个任意的实数向量且满足k T k＝1,k T 1d＝0。同时,根据公式(6.2.6)得到F 1＝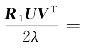

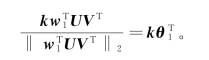
(2)当l＝2时,公式(6.2.8)为

根据公式(6.2.7)和R 1＝得到

如果公式(6.2.9)两边左乘矩阵k T,可以得到

使用η1和R 1简化如上公式,可以得到

通过定理6.1.1得到H 1＝I D－UU T w 1且w 2是矩阵H 1UV T VU T最大特征值对应的单位特征向量,则k T R 2＝δw T2,其中δ是一个任意的实数。存在解因此F 2＝

(3)当l＝3时,公式(6.2.8)为

根据R 1＝得到

通过公式(6.2.7)可得

记W 2＝(w 1,w 2),则

如果公式(6.2.10)两边分别左乘k T,根据公式(6.2.11),左边等于则k T RUV T VU T H 2＝(2λ)2 k T R。根据定理6.1.1,w 3是H 2UV T VU T最大特征值相关的单位特征向量,则k T R 3＝其中δ是一个任意的实数。存在解R 3＝因此(www.daowen.com)

类似地,对于优化问题(6.2.3),存在解R l＝(l＝1,2,…,r),其中k＝(k 1,k 2,…,k d)T是一个任意的实数向量且满足k T k＝1,k T 1d＝0。这个解也满足且

因此,这个解也是优化问题(6.2.2)的解。

注6.2.2　当因变量和自变量都是成分数据时,本节提出的单形上的PLS回归需考虑优化问题(6.2.2)。这与文献[28,95,96,107]是不同的。首先,先前文献的PLS模型都是在实数空间上研究的。其次,文献[28,96,107]考虑了基于成分自变量和实数因变量的PLS模型,文献[95]研究了基于成分自变量和一个成分因变量的PLS模型。

注6.2.3　目标优化(6.2.2)有很多解。定理6.2.1中的解R l＝(l＝1,2,…,r)为其中存在的一种解。在这个解下,目标优化(6.2.2)和(6.1.1)有相同的目标函数值,即因此当d取不同值时优化目标函数值是不变的。为了方便,取d为最小值2,即成分变量的PLS因子有两个成分。

得到权重矩阵R l和F l后,样本数据集S l和T l是已知的。建立成分变量y j(j＝1,2,…,p)和PLS因子s 1,s 2,…,s r之间的线性回归

其中B jl(l＝1,2,…,r)是一个C j×d参数矩阵且满足B jl 1d＝0Cj,E j是一个成分误差项矩阵。因为和所以上面的回归方程没有截距项。在公式(6.2.12)两边分别取ilr坐标,根据公式(2.3.3)得到

通过最小二乘方法,可得

最后,根据性质2.3.2,因为B^jl 1d＝0Cj,预测的因变量成分数据集为

定理6.2.4　在定理6.2.1中的解存在的条件下,基于成分变量的PLS回归模型(6.2.14)的估计的回归系数矩阵与基于clr系数的PLS回归模型(6.1.5)的估计的回归系数是相同的,即

证明　如果公式(6.2.13)两边分别右乘矩阵

G Cj＝(clr(Y j))T＝公式(6.2.13)简化为

根据定理6.2.1和公式(6.2.1),对于l＝1,2,…,r,得到

因此

上面的等式两边分别左乘

因为k T＝1,可以得到

与公式(6.1.4)相比,我们有

因为左边矩阵是可逆的,所以(l＝1,2,…,r),因此

定理6.2.4与每个clr系数对应于原始成分这个事实一致,即它通过原始成分关于其他成分几何均值的对数比率解释了原始成分的所有相对信息。

对公式(6.2.14)两边分别取clr系数,通过公式(6.2.1)和定理(6.2.4),可以得到

其中的定义在公式(6.1.5)中。通过公式(2.4.5),可得

则

对于本节提出的单形上的回归模型,考虑如下定义的判定系数公式(6.2.15)中的判定系数R 2等于公式(6.1.6)中的判定系数。这进一步支持了本节提出的单形上的PLS回归模型和基于clr系数的模型的等价性。