本节通过模拟分析来验证异方差线性回归模型中使用本章提出的方法相比普通最小二乘方法(OLS)表现更优。当成分误差项的ilr坐标的方差矩阵分别通过HC0,HC1,HC2,HC3,HC4和HC4m方法进行估计时,本章提出的方法类似被记为HC0,HC1,HC2,HC3,HC4和HC4m。

模拟具有一个成分因变量和两个成分自变量的线性回归模型。首先生成实数数据集U＝[u ij]2×n和V＝[v ij]2×n。U的每一列是从多元正态分布N 2(μ,Σ)中随机产生,其中μ＝(－1,1)T,Σ＝[0.3|i－j|]2×2。V中的元素是从区间[－1,1]上的均匀分布中产生。实数空间上的误差项数据集为e＝[e ij]2×n,其中e ij＝exp{γ(u 1j＋u 2j)}t ij,t ij是从标准正态分布中随机产生的。然后两个中心化的成分自变量数据集X 1和X 2可以通过如下等式得到

成分误差项ε可以通过e的ilr逆变换得到,即ε＝ilr－1(e)。最后,成分因变量Y通过如下模型得到

设置

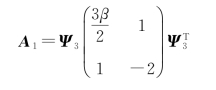
其中Ψ3是一个3×2的对比矩阵。因为Ψ3每一列求和为零,所以矩阵A 1和A 2满足每行每列分别求和都为零。在这里,我们想检验A 1中第一个参数是否等于零,这等价于检验β是否为零,即考虑假设检验

H 0:β＝0　VS　H 1:β≠0

在这个模拟中取β＝－0.50,－0.33,－0.17,0,0.17,0.33,0.50。当β＝0时,因变量数据是从原假设中产生的,否则,是从备择假设中产生的。为了体现不同的异方差程度,考虑γ＝0.0,0.3,0.6,0.9。当γ＝0.0时,误差项是同方差的,否则,它们是异方差的。对于每种设定重复1000次模拟,通过两种评价指标来进行比较。一种指标是参数估计的l 2损失‖vec(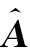)－vec(A)‖2,其中A＝(A 1,A 2),而且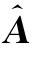是A的估计,这个测度反映了估计精度。另一种反映假设检验精度的指标是检验H 0:β＝0 VS H 1:β≠0(α＝5%)的拒绝率,检验统计量见公式(5.2.2)。

当样本量n＝50时,不同方法的两种评价指标的结果分别见表5.3.1和表5.3.2。从表5.3.1中可以发现不管β的取值是多少,当γ＝0.0,即没有异方差时,OLS方法相比其他方法有小的参数估计误差。当γ＝0.3,0.6和0.9时,HC0,HC1,HC2,HC3,HC4和HC4m方法相比OLS方法表现更优,而且它们的估计精度非常接近。随着γ增加,HC0,HC1,HC2,HC3,HC4和HC4m方法的参数估计误差越来越小,然而OLS方法的表现越来越差。表5.3.2给出的是检验H 0:β＝0　VS　H 1:β≠0(α＝5%)的拒绝率。当β＝0时,HC3方法犯第一类错误的概率相比其他方法更接近于5%。当原假设和备择假设之间的差异增加,即β远离0时,每种方法检验的势都在增加。而且,随着γ的增加,每种方法检验的势变弱。我们还计算了当样本量分别是n＝100和150时的两种评价指标,结果见表5.3.3至表5.3.6。从这些表中可以得到与表5.3.1和表5.3.2相同的结论。此外,当样本量增加时,每种方法的参数估计误差变小,每种方法检验的势都变大。总而言之,在研究基于成分因变量和成分自变量的异方差线性回归模型时,推荐使用HC 3方法。

表5.3.1　样本量n＝50时,OLS,HC0,HC1,HC2,HC3,HC4和HC4m方法的参数估计的l 2损失‖vec(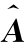)－vec(A)‖2

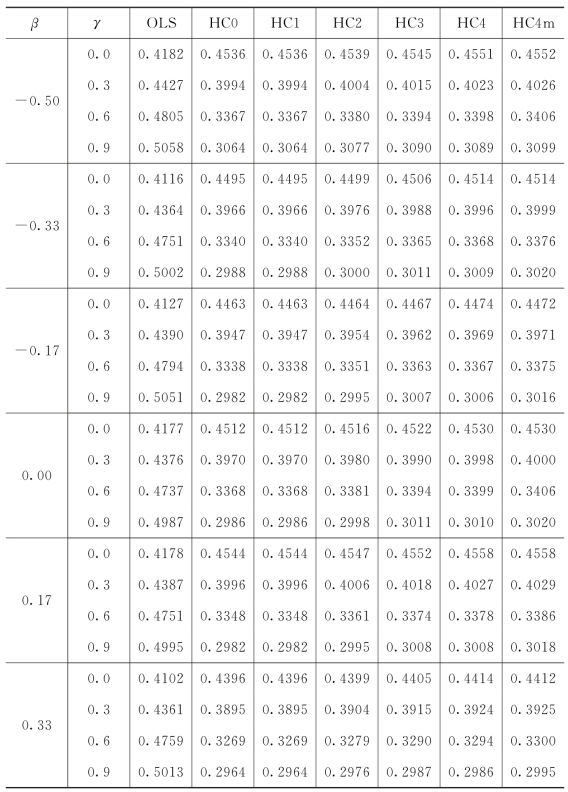
续表

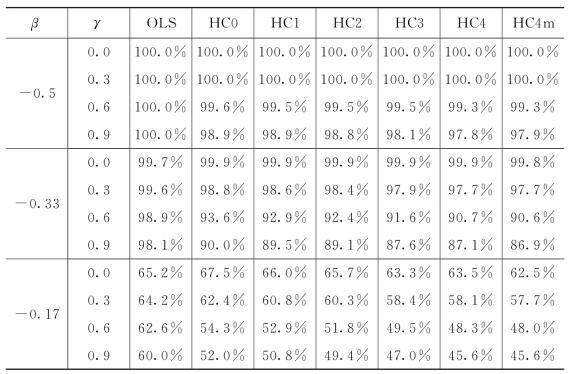
表5.3.2　样本量n＝50时,OLS,HC0,HC1,HC2,HC3,HC4和HC4m方法检验H 0:β＝0　VS　H 1:β≠0(α＝5%)的拒绝率

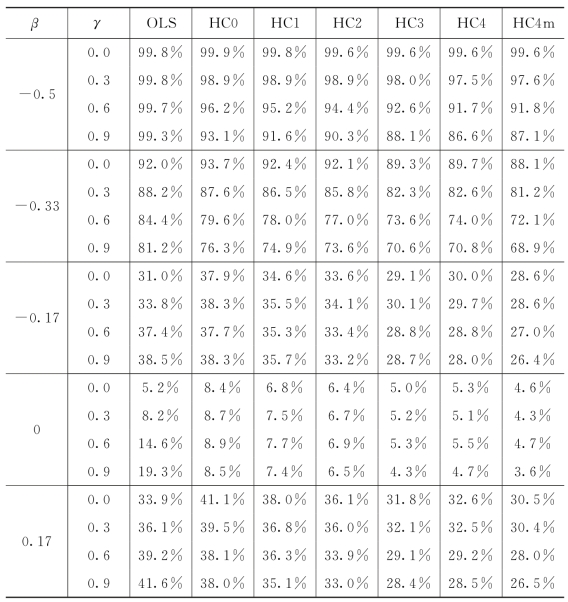
续表(www.daowen.com)

表5.3.3　样本量n＝100时,OLS,HC0,HC1,HC2,HC3,HC4和HC4m方法的参数估计的l 2损失‖vec )－vec(A)‖2

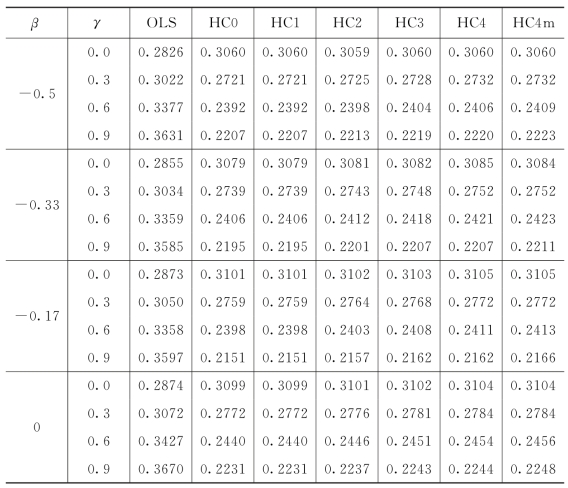
续表

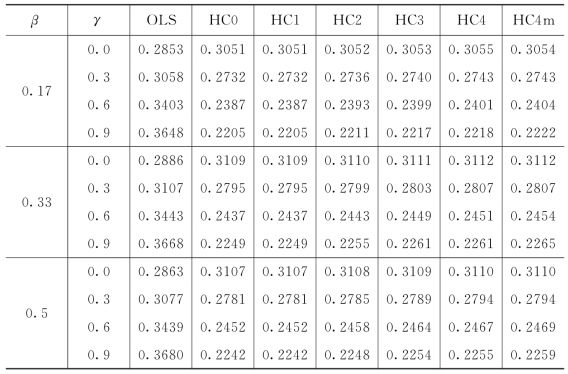
表5.3.4　样本量n＝100时,OLS,HC0,HC1,HC2,HC3,HC4和HC4m方法检验H 0:β＝0　VS　H 1:β≠0(α＝5%)的拒绝率

续表

表5.3.5　样本量n＝150时,OLS,HC0,HC1,HC2,HC3,HC4和HC4m方法的参数估计的l 2损失‖vec 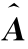)－vec(A)‖2

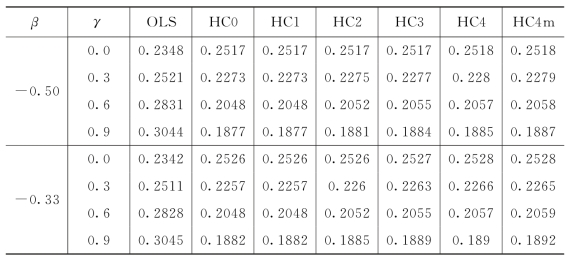
续表

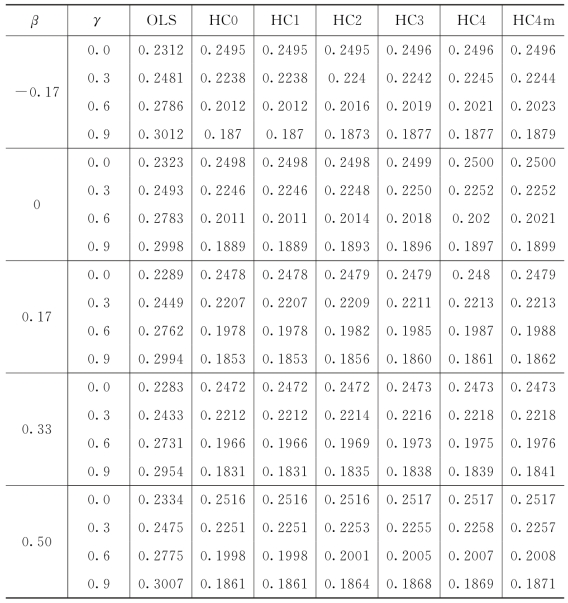
表5.3.6　样本量n＝150时,OLS,HC0,HC1,HC2,HC3,HC4和HC4m方法检验H 0:β＝0　VS　H 1:β≠0(α＝5%)的拒绝率

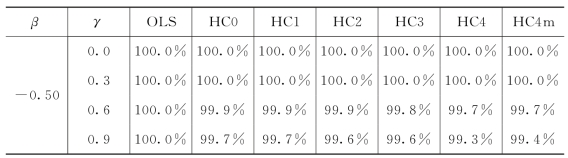
续表