根据定理4.3.2可知

因此模型(5.1.1)的参数矩阵A的显著性检验结果可以通过模型(5.1.8)中参数矩阵B的推论获得。

参数估计量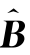可以表示为

因为成分误差项εi中心为C(1,1,…,1)T,根据成分数据的期望和成分数据的ilr坐标的期望之间的关系(见2.4节),可得E(ilr))＝0L－1。因此E()＝B,即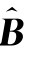是B的一个无偏估计。但B^不是B的唯一的无偏估计,普通最小二乘估计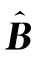OLS也是B的一个无偏估计。为简单起见,使用普通最小二乘估计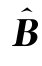OLS来进行B中参数的显著性检验。接下来求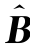OLS的方差。

引理5.2.1　给定p维随机变量和q维常数列向量b,则

其中vec是拉直运算,⊗是克罗克内积。

证明　假定b＝(b 1,b 2,…,b q)T,则

记矩阵＝C＝(c 1,c 2,…,c n)T,其中(i＝1,2,…,n)为矩阵的第i行。基于引理5.2.1,的方差为

倒数第二个等式成立是因为cov(ilr((i≠j)。

考虑vec(B)的第m(m＝1,2,…,(L－1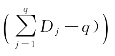个参数的假设检验

检验统计量为

其中的第m个对角元素。检验统计量τm在原假设下服从渐进N(0,1)分布[105]。

根据公式(5.2.1),我们感兴趣的是检验统计量τk j(k j＝(L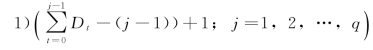－,其中D 0＝0。这些检验

统计量具有置换不变性,见如下定理。

定理5.2.2　当成分自变量(j＝1,2,…,q)中除了第一个成分外的其余成分进行任意置换时,检验统计量τk 1,τk 2,…,τk q是不变的。

证明　假设成分自变量(j＝1,2,…,q)的成分通过一个D j×D j的置换矩阵Q j进行置换,其中Q j的第一行第一列的元素为1。基于ilr坐标与clr系数之间的关系可以得到(www.daowen.com)

记－q,构造一个D×D矩阵

当所有成分自变量的成分分别都被任意置换后,对应的回归方程为

其中B Q是回归系数矩阵。由公式(5.2.3)可知则B Q的普通最小二乘估计为

倒数第二个等号是基于Q矩阵是正交矩阵得到的。

因为的第一个成分没有被置换,则矩阵的第一个元素为1,于是有(j＝1,2,…,q)。因此

而且

所以对应的检验统计量τk 1,τk 2,…,τk q是不变的。

当计算公式(5.1.10)中的权重w i以及公式(5.2.2)中的检验统计量τm时,首先需要知道(i＝1,2,…,n)。参考HC0[101],HC1[102],HC2[103],HC3[104],HC4[105]和HC4m[106]方法,可以得到Σi＝var(ilr

其中h i是矩阵的第i个对角元素,γ1和γ2为正实数。当γ1＝1.0,γ2＝1.5时,可以得到HC4m估计的最佳一致逼近[106]。

根据定理5.1.1和公式(5.2.2),可以获得实数空间上模型(5.1.8)中B＝的估计和假设检验。基于公式(5.2.1),可得本章研究的单形上模型(5.1.1)中A 1,A 2,…,A q的估计和推论,即得到因此,因变量中心为

上式两边分别取clr系数可以得到

其中(j＝1,2,…,q)中第l(l＝1,2,…,L)行第k(k＝1,2,…,D j)列的参数反映了x j的第k个成分的所有相对信息对因变量中心的第l个成分的所有相对信息的影响。

最后,预测的成分数据集为

考虑均方根距离

作为模型的评价指标,小的RMSD代表模型有高的预测精度。