考虑基于成分因变量y∈S L和成分自变量x 1∈S D 1,x 2∈S D 2,…,x q∈S Dq的多元线性回归模型[97]

其中Y＝(y 1,y 2,…,y n),X j＝(x 1j,x 2j,…,x nj)(j＝1,2,…,q)分别为中心化后的有n个观测值的样本数据集,A 1,A 2,…,A q为参数矩阵且满足A j 1Dj＝0L(j＝1,2,…,q)。成分误差项为ε＝(ε1,ε2,…,εn),其中εi(εi∈S L(i＝1,2,…,n))中心为C(1,1,…,1)T,即cen(εi)＝C(1,1,…,1)T。如果var(ilr(ε1)),var(ilr(ε2)),…,var(ilr(εn))不完全相等,则成分误差项具有异方差性。接下来,分别给出模型(5.1.1)中参数的估计和推论。

通过加权最小二乘方法可以估计异方差模型(5.1.1)中的参数矩阵。目标函数为

其中w i为权重。通过最小化目标函数Q(A 1,A 2,…,A q)关于A k(k＝1,2,…,q)可获得估计量记对角矩阵W＝diag(w 1,w 2,…,w n),根据

可以得到

记(clr(X 2))T,…,(clr(X q))T)T,V clr＝clr(Y)公式(5.1.2)可以简化为

由于clr系数求和为零,因此矩阵U clr W(U clr)T是奇异的,则公式(5.1.3)不能给出A^的显示表达式。因此,需要通过公式(5.1.3)来推导实数空间上异方差回归模型的参数估计。

对回归模型(5.1.1)两边分别取ilr坐标,根据公式(2.3.3)可以得到

基于置换后的成分数据的定义(见定义2.1.5),记Y(l 0)＝(j＝1,2,…,q)分别为置换后的成分数据集,置换后的成分误差项为ε(l 0)＝根据公式(2.3.3),置换后的成分数据集的ilr坐标与原始成分数据集的ilr坐标之间的关系为

由于ΨL为正交矩阵(见公式(4.2.5)),则

基于关系式(5.1.4)和(5.1.5)可以得到

其中第三个等号和第五个等号是基于关系式G Dj和G L A j＝A j G Dj＝A j(j＝1,2,…,q)得到的。

记V ilr＝ilr(Y(l 0)),U ilr＝((ilr(,…,其中

公式(5.1.6)可以简化为

根据公式(5.1.5)有(www.daowen.com)

由于

ΨL是正交矩阵,如果var(ilr(ε1)),var(ilr(ε2)),…var(ilr(εn))不完全相同,则var(ilr()),var(ilr()),…var(ilr))不完全相同。因此,模型(5.1.8)的异方差误差项即var(ilr))彼此不完全相同。

定理5.1.1　虑异方差线性回归模型(5.1.8),参数矩阵B的估计量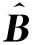可以通过下面的表达式得到

证明　参数矩阵和A j之间的关系为

基于关系式＝G Dj和A j G Dj＝A j可得

记为估计的参数矩阵,且

我们有

对上面等式两端分别右乘矩阵U clr W(U clr)T P T,则

由于

则等式(5.1.9)左边等于B^U ilr WU Tilr,右边等于

第一个等号是基于公式(5.1.3)得到的。因此,公式(5.1.9)可以简化为

通过定理5.1.1可以得到回归系数矩阵B的估计,基于公式(5.1.7)进而可以得到A 1,A 2,…,A q的估计。根据成分数据的总方差和成分数据的ilr坐标的方差之间的关系(见2.4节),可得

因此本章选择权重