实数空间上基于ilr坐标的多元线性回归模型为

其中ilr(v i),ilr(u ji)分别代表的是因变量v i和自变量u ji(j＝1,2,…,q)的ilr坐标,b 0,B 1,…,B q为模型的参数,ilr(εi)为随机误差项,服从多元正态分布,均值为0L－1且具有相同的协方差阵。使用最小二乘法,参数b 0,B 1,…,B q的估计值可以通过如下方程来求解

下面的定理给出了单形上的回归模型与实数空间上的回归模型的参数之间的关系。

定理4.2.1　模型(4.1.1)的参数a 0,A 1,…,A q和模型(4.2.1)的参数b 0,B 1,…,B q具有如下关系:

对应的参数估计值之间的关系为

证明　分别对模型(4.1.1)两边做ilr变换,根据性质2.2.5和公式(2.3.3)可得

与模型(4.2.1)进行对照,可以得到b 0＝ilr(a 0),B j＝1,2,…,q)。由于＝G Dj且G L A j G Dj＝A j,所以a 0＝ilr－1(b 0),A j＝ΨL B j(j＝1,2,…,q)。

根据ilr坐标和clr系数之间的关系(公式2.2.3)可以得到

因此公式(4.2.2)可以化简为

上面的方程两边分别右乘矩阵＝G L且(clr(v i))T G L＝(clr(v i))T,对应于公式(4.1.2),我们有

参数矩阵B j(j＝1,2,…,q)第一行第一列的元素解释了u j的第一个ilr坐标ilr(u j)1对v的第一个ilr坐标ilr(v)1的影响,即反映了u j的第一个成分的相对信息对v的第一个成分的相对信息的影响。然而,其他参数不能反映u j的剩余成分的相对信息对v的剩余成分的相对信息的影响。为了反映u j的每个成分的相对信息对v的每个成分的相对信息的影响,需要置换u j以及v的成分。当成分因变量和成分自变量的成分分别置换以后,模型(4.2.1)可以表示为:

其中ilr分别为置换后的成分的ilr坐标,置换后的成分的定义见定义1.1.5,截距向量,(j＝1,2,…,q)是回归系数矩阵。特别地,当模型(4.2.3)中l 0＝l 1＝…＝l q＝1时,可以得到模型(4.2.1)。在下面的定理中,可以看到模型(4.2.3)的截距向量和回归系数矩阵可以通过模型(4.2.1)的参数来表示。(www.daowen.com)

定理4.2.2　模型(4.2.1)的参数b 0,B 1,…,B q与模型(4.2.3)的参数具有如下关系

其中P L,l 0为置换矩阵。

证明　对于任意的成分数据v(v∈S L),根据公式(2.2.3)可以得到

则模型(4.2.1)可以简化为

由于置换矩阵满足J L＝J L,则

因此为正交矩阵。如果等式(4.2.4)两边分别左乘矩阵P L,l 0ΨL,则可以得到

通过与模型(4.2.3)进行对照,很容易得到

模型(4.2.3)是一个经典的多因变量回归模型。我们主要关注矩阵(j＝1,2,…,q)中第一行第一列的参数的解释,即感兴趣的是因变量ilr(v(l 0))的第一个变量,记为,其中e L－1,1＝(1,0,0,…,0)T,所以我们仅研究如下模型

记l＝(l 0,l 1,…,l q),及

其中D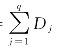＝－q,模型(4.2.6)可以简化为

通过最小二乘法可以得到