对于有D个部分的成分数据变量,如果有n个观测值,则数据集可以记为
其中成分数据集X的每一行为一个成分数据,每一列x j(j=1,2,…,D)是由所有n个成分数据的第j个成分组成的。假定成分数据集X有近似零值,近似零值是由于观测值低于已知的探测范围而产生的,而且不同成分数据相同部分的探测范围是相同的。对应的探测范围可以被记为e=(e 1,e 2,…,e D)T,其中e j是第j个成分x j的探测范围,且事先已知。
首先,通过乘法替换法对近似零值进行初始化,其中近似零值等于探测范围乘以65%。
在这种情况下,协方差结构的扭曲最小[56]。然后对X的所有部分进行Q型聚类分析[18,93],其中X的方差矩阵为不相似矩阵[19]。方差矩阵中每行每列的元素为任意两个成分的对数比率的方差。聚类分析的目的是使得相似的部分被放在相同的类中,不相似的部分被放在不同的类中。假定通过某个准则得到聚类个数为g,最后根据每类中的部分数得到g类子成分数据集X 1,X 2,…,X g,
其中x k j(k j∈{1,2,…,D})是X k中的第j个成分。记M k⊂{1,2,…,n}为X k中有近似零值的成分观测指标,M k,i⊂{1,2,…,D k}为X k的第i个观测值中有近似零值的部分指标,则O k,i={1,2,…,D k}\M k,i指的是剩余部分指标。换句话说,M k对应数据集X k的行指标,M k,i和O k,i对应数据集X k的列指标。
接下来,替换子成分数据集X k(k∈{1,2,…,g})中的近似零值。首先,数据集X k通过clr变换得到clr系数U k=clr(X k)=(u k,1,u k,2,…,u k,Dk)=[u k,ij]n×Dk。对于第i(i∈M k)个观测值,近似
零值x ik j<e k j(j∈M k,i)导致未知数u k,ij小于ψk,ij,其中
ψk,ij是探测范围第k j个元素对应的clr系数。记X-k=(X 1,…,X k-1,X k+1,…,X g),U-k为X-k的clr系数,然后使用偏最小二乘回归[94]来建立因变量U k和自变量U-k的线性关系
其中![]() =(βk,01,βk,02,…,βk,0Dk)是截距项,βk=(βk,1,βk,2,…,βk,Dk)是回归系数,ϵk=(ϵk,1,ϵk,2,…,ϵk,Dk)为误差项矩阵,1n为元素全为1的列向量。因变量U k和自变量U-k的关系不能直接通过公式(3.2.2)发现。事实上,因变量U k和自变量U-k可以通过潜变量建模,分别根据以下模型确定
=(βk,01,βk,02,…,βk,0Dk)是截距项,βk=(βk,1,βk,2,…,βk,Dk)是回归系数,ϵk=(ϵk,1,ϵk,2,…,ϵk,Dk)为误差项矩阵,1n为元素全为1的列向量。因变量U k和自变量U-k的关系不能直接通过公式(3.2.2)发现。事实上,因变量U k和自变量U-k可以通过潜变量建模,分别根据以下模型确定
其中T 1和T 2是n×r(r≤min(D k,D-D k,n))得分矩阵,P 1和P 2是载荷矩阵,E 1和E 2是误差矩阵。通过最大化有约束的协方差来获得得分矩阵T 1和T 2[94]。对于求解偏最小二乘回归问题,很多算法可以估计公式(3.2.2)中的回归系数。
通过公式(3.2.2)可得
根据文献[58,59],未知数u k,ij插补为
其中u-k,i指的是U-k的第i行,正态分布N(0,1)的分布函数和密度函数分别记为Φ(·)和φ(·),![]() 是变量u k,j在条件变量U-k下的估计方差的平方根。公式(3.2.4)的插补值
是变量u k,j在条件变量U-k下的估计方差的平方根。公式(3.2.4)的插补值![]() 是通过正态性假定下简化期望E(u k,ij|u-k,i,u k,ij<ψk,ij)得到的[58]。根据
是通过正态性假定下简化期望E(u k,ij|u-k,i,u k,ij<ψk,ij)得到的[58]。根据
可知插补值![]() 小于临界值ψk,ij。
小于临界值ψk,ij。
因为clr系数求和为零,所以需要调整已知的数据u k,ij(i∈M k,j∈O k,i)。对于任意的j,l∈O k,i,成分x ik j和成分x ik l没有零值,因此比率x ik j/x ik l是不变的。由于u k,ij-u k,il=ln(x ik j/x ik l),修正后的数据![]() 需要满足
需要满足
当j固定,l在O k,i中变动时,上面不同等式的和为
其中![]() 为集合O k,i的基数。根据
为集合O k,i的基数。根据![]() =0,公式(3.2.5)可以简化为
=0,公式(3.2.5)可以简化为
记U k替换后的数据集为![]() 其中
其中![]() =u k,ij(i∈{1,2,…,n}\M k)。
=u k,ij(i∈{1,2,…,n}\M k)。![]() 通过clr逆变换后的数据集为
通过clr逆变换后的数据集为![]() =
=![]() 为了得到原始的尺度,应该重新调整值
为了得到原始的尺度,应该重新调整值![]() (i∈M k,j∈M k,i)。最后,近似零值x ik j(i∈M k,j∈M k,i)应该替换为以下表达式[63]
(i∈M k,j∈M k,i)。最后,近似零值x ik j(i∈M k,j∈M k,i)应该替换为以下表达式[63]
其中x ik l(l∈O k,i)为原始不是近似零值的值。公式(3.2.7)将插补值调整为数据的原始尺度。
该方法的具体步骤如下:
Step 1 通过乘法替换方法对近似零值进行初始化。
Step 2 对X进行Q型聚类分析得到g类部分,对应于g个子成分数据集X 1,X 2,…,X g。通过每一类中近似零值的比例对g类进行降序排列。不失一般性,假定g类已经排好序,即第一类中近似零值比例最高,其次是第二类,第g类中近似零值比例最低。
Step 3 设置k=1。
Step 4 记X-k=(X 1,…,X k-1,X k+1,…,X g),而且X k和X-k的clr系数分别为U k和U-k。建立U k和U-k的偏最小二乘回归,然后通过公式(3.2.4)插补未知数据u k,ij(i∈M k,j∈M k,i),通过公式(3.2.6)调整已知数据u k,ij(i∈M k,j∈O k,i)。
Step 5 对插补后的数据集进行clr逆变换。最后,通过公式(3.2.7)替换近似零值x ik j(i∈M k,j∈M k,i)。
Step 6 对于每个有近似零值的子成分数据集X k对应的k(k∈{2,3,…,g})执行Steps 4~5。
Step 7 重复Steps 3~6直到上一步迭代和下一步迭代中每一类X k(k=1,2,…,g)的clr系数的元素平方差之和小于一个非常小的数。
Step 8 按成分部分原始的顺序对g类部分重新进行排序。(www.daowen.com)
虽然算法的收敛性没有给出证明,但是在模拟和实例分析中提出的算法通常在几次迭代后收敛。在算法的每一步中(参见算法Step 3的指标k),通过公式(3.2.1),算法从对应的探测范围值e k j计算出对应的ψk,ij值,之后在每一步这个值被逆变换到单形上。由于ψk,ij和e k j的单调对应关系,clr系数的插补值低于ψk,ij,对应于原始尺度数据近似零值的替换值低于e k j。实践经验也反映了这一点,即本节提出的方法的近似零值的替换值是低于对应的探测范围值的。
定理3.2.1 在偏最小二乘回归(3.2.3)中,因变量为X k的clr系数或ilr坐标能得到等价的结果。此外,在两种坐标系统下,公式(3.2.4)可以产生等价的结果。
证明 基于简单偏最小二乘算法来求解偏最小二乘问题。为了建立u k和u-k的偏最小二乘回归,首先考虑优化问题
其中w(c)l,θ(c)l(l=1,2,…,r)为权重向量,下标(c)表示u k是成分变量x k的clr系数,r指的是给定的偏最小二乘因子数。记W(c)r=(w(c)1,w(c)2,…,w(c)r),则由偏最小二乘因子构成的数据矩阵为F(c)=(U-k w(c)1,U-k w(c)2,…,U-k w(c)r)=U-k W(c)r。
同样,使用![]() 的ilr坐标为因变量,记为
的ilr坐标为因变量,记为![]()
![]() 其中
其中![]() 是X k置换后的成分数据集。建立
是X k置换后的成分数据集。建立![]() 的偏最小二乘回归,优化问题为
的偏最小二乘回归,优化问题为
其中w(i)l,θ(i)l(l=1,2,…,r)是权重向量,下标(i)代表![]() 是成分变量
是成分变量![]() 的ilr坐标。由偏最小二乘因子构成的数据矩阵为F(i)=(U-k w(i)1,U-k w(i)2,…,U-k w(i)r)=U-k W(i)r,其中W(i)r=(w(i)1,w(i)2,…,w(i)r)。
的ilr坐标。由偏最小二乘因子构成的数据矩阵为F(i)=(U-k w(i)1,U-k w(i)2,…,U-k w(i)r)=U-k W(i)r,其中W(i)r=(w(i)1,w(i)2,…,w(i)r)。
对于公式(3.2.8)和公式(3.2.9)的优化问题,权重向量可以通过拉格朗日乘数法得到[95,96],w(c)l和w(i)l(l=1,2,…,r)分别为![]()
![]() 的最大特
的最大特
征值相关的单位特征向量,其中
根据clr系数和ilr坐标之间的关系可以得到
其中P是置换矩阵,ΨDk是D k×(D k-1)对比矩阵,则
因此W(c)r=W(i)r,F(c)=F(i)。
因变量U k和自变量U-k的偏最小二乘回归模型为
其中![]()
=(β(c)k,01,β(c)k,02,…,β(c)k,0Dk)是截距项,β(c)k=(β(c)k,1,β(c)k,2,…,β(c)k,Dk)是回归系数,ϵ(c)k=(ϵ(c)k,1,ϵ(c)k,2,…,ϵ(c)k,Dk)是误差项矩阵。根据文献[94],公式(3.2.10)中的回归系数估计为
其中0r是元素全为0的列向量。
同样,因变量![]() 和自变量U-k的偏最小二乘回归模型为
和自变量U-k的偏最小二乘回归模型为
其中![]() =(β(i)k,01,β(i)k,02,…,β(i)k,0Dk-1),β(i)k=(β(i)k,1,β(i)k,2,…,β(i)k,Dk-1)是参数,ϵ(i)k=(ϵ(i)k,1,ϵ(i)k,2,…ϵ(i)k,Dk-1)是误差项矩阵。公式(3.2.12)的回归系数通过下式来估计
=(β(i)k,01,β(i)k,02,…,β(i)k,0Dk-1),β(i)k=(β(i)k,1,β(i)k,2,…,β(i)k,Dk-1)是参数,ϵ(i)k=(ϵ(i)k,1,ϵ(i)k,2,…ϵ(i)k,Dk-1)是误差项矩阵。公式(3.2.12)的回归系数通过下式来估计
从公式(3.2.10)和(3.2.12)可以得到由于u k,j=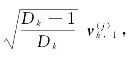 通过公式(3.2.11)和(3.2.13)可得
通过公式(3.2.11)和(3.2.13)可得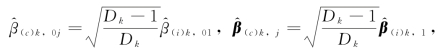 则
则
因此,在偏最小二乘回归中,因变量为clr系数或ilr坐标能得到等价的因变量值,差别在于一个尺度常数。
通过文献[58,59]和公式(3.2.14),未知数据u k,ij的插补值为
其中![]() 是u k,j在条件U-k下估计方差的平方根,u-k,i指的是U-k的第i行,N(0,1)的分布和密度函数分别记为Φ(·)和φ(·)。
是u k,j在条件U-k下估计方差的平方根,u-k,i指的是U-k的第i行,N(0,1)的分布和密度函数分别记为Φ(·)和φ(·)。
同样,使用X k的ilr坐标,近似零值x ik j<e kj导致未知数据![]() 小于
小于![]() 其中
其中
根据公式(3.2.15),未知数据![]() 的插补值为
的插补值为
其中![]() 在条件变量U-k下估计方差的平方根。
在条件变量U-k下估计方差的平方根。
现在证明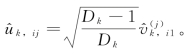 根据公式(3.2.16)可得
根据公式(3.2.16)可得
从![]() 可知
可知
因此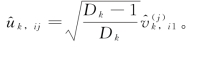
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






