本节介绍成分数据的描述性统计,包括中心和方差[86]。在实数空间上,随机变量有期望和方差,但它们不能描述成分数据的中心趋势与变化趋势。对于任意的随机变量x∈ℝ,它的方差为var(x)＝E(x－E(x))2,反映了x与期望E(x)的偏离程度。类似于实数空间,接下来给出成分数据中心与方差的定义。

定义2.4.1(随机成分的偏离程度)　对于随机成分x∈S D,给定一个成分数据z∈S D,x关于z的偏离程度为

其中E(·)为实数空间上的随机变量的期望。

定义2.4.2(成分数据的中心和总方差)　对于随机成分x∈S D,假定x的偏离程度存在,则x的中心为

x与任意z的最小偏离程度为总方差

对于随机成分x＝(x 1,x 2,…,x D)T∈S D,它的clr系数和ilr坐标为实数空间上的随机变量。记clr(x)＝(clr1(x),clr2(x),…,clr D(x))T,ilr(x)＝(ilr1(x),ilr2(x),…,ilr D－1(x))T,其中clr i(x)(i＝1,2,…,D)为clr(x)的第i个元素,ilr i(x)(i＝1,2,…,D－1)为ilr(x)的第i个元素。随机成分x的中心和总方差的等价表达式为

cen(x)＝ilr－1(E(ilr(x)))＝clr－1(E(clr(x)))＝C(exp(E(ln(x))))

如果有样本,可以根据样本信息来估计总体信息,随机成分x的中心和总方差的估计表达式为

其中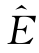(·)代表期望E(·)的估计值,代表方差var(·)的估计值。公式(2.4.1)给出了单形上样本中心与实数空间上的样本均值之间的关系。特别地,如果

首先验证成分数据中心的估计表达式(2.4.1)是否成立。对于随机成分x,假设有n个观测值x 1,x 2,…,x n,其中x i∈S D(i＝1,2,…,n)。根据clr逆变换可得

根据性质2.2.3(1)可得因此公式(2.4.1)成立。在上面的证明过程中,可以看出成分数据样本中心的定义。

定义2.4.3　随机成分x的样本中心定义为

同理,

性质2.4.4　对于随机成分x∈S D,y∈S D,给定C×D的实数矩阵A,样本中心有如下性质:

(1)

(2)

(3)如果矩阵A满足A 1D＝0C,则

证明　基于样本中心的定义来证明它的性质。

(1)根据性质2.1.3可得

(2)根据性质2.1.3可得(www.daowen.com)

(3)如果矩阵A满足A 1D＝0C,根据性质2.3.2可得

接下来验证成分数据总方差的估计表达式(2.4.2)是否成立。根据Aitchison距离以及ilr坐标的等距性可得

同理可得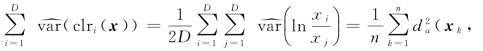因此公式(2.4.2)成立。成分数据的样本总方差定义如下。

定义2.4.5　随机成分x的样本总方差定义为

基于定义2.4.5,两个有相同部分的随机成分x与y的样本协方差为

为了后面几个章节的需要,接下来给出成分数据集上的运算以及成分数据集的对数比率变换定义。考虑两个随机成分x,y∈S D,假设它们都有n个观测值,对应的成分数据集记为

其中x i,y i∈S D(i＝1,2,…,n)。成分数据集的基本概念定义如下:

(1)扰动:X⊕Y＝(x 1⊕y 1,x 2⊕y 2,…,x n⊕y n)。

(2)幂:α⊙X＝(α⊙x 1,α⊙x 2,…,α⊙x n),其中α为实数。

(3)扰动差:X⊖Y＝(x 1⊖y 1,x 2⊖y 2,…,x n⊖y n)。

(4)Aitchison内积:

(5)Aitchison范数:‖X‖a＝〈X,X〉a。

(6)Aitchison距离:d a(X,Y)＝‖X⊖Y‖a。

(7)矩阵乘积:

(8)clr与ilr数据集:clr(X)＝(clr(x 1),clr(x 2),…,clr(x n)),ilr(X)＝(ilr(x 1),ilr(x 2),…,ilr(x n))。

(9)样本中心化:

基于以上定义,随机成分x和y的样本协方差为

根据〈x,y〉a＝(clr(x))T clr(y),成分数据集的Aitchison内积可以简化为

其中tr代表矩阵的迹。