2.2节介绍的幂运算将成分数据x∈S D映射为α⊙x∈S D。本节介绍一种单形上的线性变换,通过矩阵乘积运算将单形S D上的成分数据映射到S C上的成分数据[85]。

定义2.3.1(单形上的矩阵乘积)　对于任意成分数据x∈S D 2,给定一个D 1×D 2实数矩阵A＝[a ij]D 1×D 2,单形上的矩阵乘积定义为

单形上的矩阵乘积运算将S D 2上的x变换为S D 1上的Ax。定义2.3.1中的矩阵乘积运算还有另一种表达式

性质2.3.2　对于任意成分数据x∈S D 1,y∈S D 2,以及C×D 1的实数矩阵A和C×D 2的实数矩阵B,矩阵乘积运算有如下性质:

(1)结合性1:如果矩阵B满足B T 1C＝0D 2,

(2)结合性2:对于任意实数α,如果矩阵A满足A 1D 1＝0C,则

(3)组合性:当D 1≠D 2时,A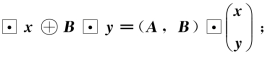

(4)分配性1:当D 1＝D 2时,

(5)分配性2:当D 1＝D 2时,如果矩阵A满足A 1D 1＝0C,则A

(6)线性性:当D 1＝D 2时,对于任意实数α和β,如果矩阵A满足A 1D 1＝0C,则

证明:根据公式(2.3.1)来证明性质2.3.2。

(1)当矩阵B满足B T 1C＝0D 2时,有(www.daowen.com)

其中k＝(A ln(x)))。

(2)如果矩阵A满足A 1D 1＝0C,则AG D 1＝A。根据性质2.2.3可知

又由于

因此结合性2的等式成立。

(3)当D 1≠D 2时,有

(4)当D 1＝D 2时,可得

(5)类似于性质2.3.2(2)的证明,得到

(6)根据结合性2和分配性2易得

对于任意成分数据x∈S D 2,给定一个D 1×D 2实数矩阵A,根据公式(2.2.3)与(2.3.1),可得Ax的clr系数及ilr坐标为

如果矩阵A满足和则公式(2.3.2)可化简为