在实数空间上,任意向量x＝(x 1,x 2,…,x D)T∈ℝD可以表示为

其中{e D,1,e D,2,…,e D,D}为ℝD上的标准正交基。根据定义1.1.3可知e D,i不是成分数据,因此它不能作为单形上的基。对于成分数据x＝(x 1,x 2,…,x D)T∈S D,我们需构造单形上的基,一种直接的方法是对e D,i取指数,得到单形上的基{w 1,w 2,…,w D}

w i＝C(exp(e D,i))＝C(1,1,…,e,…,1)T,i＝1,2,…,D

其中e在w i的第i个位置。

如果去掉第D个向量w D,考虑基{w 1,w 2,…,w D－1},则成分数据x＝(x 1,x 2,…,x D)T∈S D可以表示为

成分数据x∈S D在基{w 1,w 2,…,w D－1}上的坐标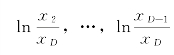对应于众所周知的非对称对数比率坐标[19],见如下定义。

定义2.2.1(非对称对数比率(alr)坐标)　对于任意成分数据x＝(x 1,x 2,…,x D)T∈S D,选取x D作为参考部分,通过alr变换将x∈S D变换为ℝD－1上的坐标,alr坐标为

记alr变换后数据为alr(x)＝ζ＝(ζ1,ζ2,…,ζD－1)T,则alr逆变换为

x＝alr－1(ζ)＝C(exp(ζ1),exp(ζ2),…,exp(ζD－1),1)T

对于x,y∈S D,α1,α2∈ℝ,alr坐标满足

alr(α1⊙x⊕α2⊙y)＝α1·alr(x)＋α2·alr(y)

alr变换选取参考部分x D作为分母,因此它是非对称的。事实上,也可以选取其他成分作为分母,分母的不同选取对分析结果没有影响。由于基{w 1,w 2,…,w D－1}中任意两个向量的Aitchison内积不为零,则{w 1,w 2,…,w D－1}为非正交基,因此alr变换不能保证从S D到ℝD－1的等距性。

如果考虑基{w 1,w 2,…,w D},则成分数据x＝(x 1,x 2,…,x D)T∈S D可以表示为

上面的表达式给出了对称对数比率系数[19],见如下定义。

定义2.2.2(对称对数比率(clr)系数)　对于任意成分数据x＝(x 1,x 2,…,x D)T∈S D,通过clr变换将x∈S D变换为ℝD上的系数,clr系数为

记clr变换后数据为clr(x)＝ξ＝(ξ1,ξ2,…,ξD)T,则clr逆变换为

x＝clr－1(ξ)＝C(exp(ξ1),exp(ξ2),…,exp(ξD))T

性质2.2.3　对于x,y∈S D,α,β∈ℝ,clr系数满足

(1)clr(α⊙x⊕β⊙y)＝α·clr(x)＋β·clr(y);

(2)〈x,y〉a＝〈clr(x),clr(y)〉;

(3)‖x‖a＝‖clr(x)‖,d a(x,y)＝d(clr(x),clr(y))。其中〈·〉,‖·‖,d(·,·)分别代表实数空间上的内积、范数、距离。

clr变换关于成分是对称的,但是变换后的数据求和为零,与之相对应的协方差矩阵是奇异的。从性质2.2.3可以看出,clr变换可以保证从S D到ℝD－1的等距性,即clr系数间的欧氏距离与原始成分数据间的Aitchison距离相等。

由于基{w 1,w 2,…,w D－1}为非正交基,因此可通过施密特正交化转化为正交基且正交基不唯一[15]。假设单形S D上的正交基为{e 1,e 2,…,e D－1},成分数据x＝(x 1,x 2,…,x D)T∈S D在正交基上可以表示为

成分数据x∈S D在正交基{e 1,e 2,…,e D－1}上的坐标〈x,e 1〉a,〈x,e 2〉a,…,〈x,e D－1〉a对应于等距对数比率坐标[15],见如下定义。

定义2.2.4(等距对数比率(ilr)坐标)　对于任意成分数据x＝(x 1,x 2,…,x D)T∈S D,给定单形S D上的正交基{e 1,e 2,…,e D－1},通过ilr变换将x∈S D变换为ℝD－1上的坐标,ilr坐标为

ilr(x)＝(〈x,e 1〉a,〈x,e 2〉a,…,〈x,e D－1〉a)T

性质2.2.5　对于x,y∈S D,α,β∈ℝ,ilr坐标满足

(1)ilr(α⊙x⊕β⊙y)＝α·ilr(x)＋β·ilr(y);

(2)〈x,y〉a＝〈ilr(x),ilr(y)〉;

(3)‖x‖a＝‖ilr(x)‖,d a(x,y)＝d(ilr(x),ilr(y))。从性质2.2.5可以看出,ilr变换可以保证从S D到ℝD－1的等距性。虽然clr变换也是等距的,但是clr系数有求和为零的约束。

给定单形上的正交基{e 1,e 2,…,e D－1},记ψi＝clr(e i),i＝1,2,…,D－1,对比矩阵ΨD＝[ψij]D×(D－1)＝(ψ1,ψ2,…,ψD－1)是一个D×(D－1)矩阵。根据性质2.2.3可得

〈e i,e j〉a＝〈clr(e i),clr(e j)〉＝δij

当i＝j时,δij＝1,否则,δij＝0。矩阵ΨD满足

证明　下面给出公式(2.2.1)的证明。公式(2.2.1)中I D为单位矩阵,1D为元素全为1的列向量,0D－1为元素全为0的列向量。(www.daowen.com)

根据矩阵ΨD中ψi之间的正交性可得由于ψi中元素求和为零,则假定

其中M是一个常数m矩阵。公式(2.2.2)两边分别左乘矩阵可得

同样公式(2.2.2)两边分别右乘ΨD可得

因此ΨD是的伪逆矩阵。

此外

且

其中tr代表矩阵的迹,因此m＝－

由于〈x,e i〉a＝〈clr(x),clr(e i)〉＝(clr(e i))T clr(x)＝ψT i clr(x),因此结合公式(2.2.1),ilr坐标与clr系数有如下关系

公式(2.2.3)第一个等号两边左乘ΨD可得

记ilr变换后数据为ilr(x)＝x*＝则ilr逆变换为

从公式(2.2.3)可以看出,ilr坐标也可以根据ilr(x)＝n(x)来确定。由于基{w 1,w 2,…,w D－1}通过施密特正交化得到的单形S D上的正交基为{e 1,e 2,…,e D－1}且不唯一,因此对应的矩阵ΨD不唯一,相应的ilr坐标有多种形式。接下来介绍一种顺序二进制划分方法来确定矩阵ΨD。该方法总共进行D－1次划分,每次划分将成分进行二分类,一类记为＋1,另一类记为－1。假定在第j次划分时,有r个成分部分{i 1,i 2,…,i r}为＋1类,s个成分部分{j 1,j 2,…,j s}为－1类,则

因此ilr坐标的第j个元素为

对于成分数据x＝(x 1,x 2,x 3,x 4,x 5)T∈S 5,考虑如下两种划分情形:

情形一:成分数据x的部分进行四次划分(一)

第一次划分将子成分{x 1,x 2,x 3,x 4,x 5}分为两类,{x 1,x 2,x 5}为＋1类(r＝3),{x 3,x 4}为－1类(s＝2);

第二次划分将子成分{x 1,x 2,x 5}分为两类,{x 1}为＋1类(r＝1),{x 2,x 5}为－1类(s＝2);

第三次划分将子成分{x 2,x 5}分为两类,{x 2}为＋1类(r＝1),{x 5}为－1类(s＝1);

第四次划分将子成分{x 3,x 4}分为两类,{x 3}为＋1类(r＝1),{x 4}为－1类(s＝1)。

四次划分对应的矩阵Ψ5＝[ψij]5×4为

与之相对应的ilr坐标为

情形二:成分数据x的部分进行四次划分(二)

第一次划分将所有成分{x 1,x 2,x 3,x 4,x 5}分为两类,{x 1}为＋1类(r＝1),{x 2,x 3,x 4,x 5}为－1类(s＝4);

第二次划分将子成分{x 2,x 3,x 4,x 5}分为两类,{x 2}为＋1类(r＝1),{x 3,x 4,x 5}为－1类(s＝3);

第三次划分将子成分{x 3,x 4,x 5}分为两类,{x 3}为＋1类(r＝1),{x 4,x 5}为－1类(s＝2);

第四次划分将子成分{x 4,x 5}分为两类,{x 4}为＋1类(r＝1),{x 5}为－1类(s＝1)。

四次划分对应的矩阵Ψ5＝[ψij]5×4为

与之相对应的ilr坐标为

情形二的划分有一定的规律,每次将某一个成分划分为一类,其余成分为另一类。如果将情形二的划分推广到D个部分,则可得到

与之相对应的ilr坐标为

在这种坐标形式下,ilr逆变换可以将任意实数向量x*∈ℝD－1变换为原始成分x,具体形式为

成分数据可以看成等价类,因此最后得到的成分数据x可以表示为具有常数和约束的向量。

成分部分的不同划分对应不同的ilr坐标形式,例如情形一与情形二。公式(2.2.5)的ilr坐标形式被广泛地使用,因为ilr坐标的第1个元素反映了成分数据x中成分x 1所解释的相对信息。本书的ilr坐标都采用了公式(2.2.5)的形式。