记因变量为y,自变量为x。根据y或x是否为成分数据,可以将回归分析分为三种类型:第一种类型中y为实数数据,x为成分数据;第二种类型中y为成分数据,x为实数数据;第三种类型中所有的y和x都是成分数据。近年来,这三种类型已引起了很多学者的关注,他们提出了许多相应的模型。下面分别介绍每种类型已有的回归分析模型。

1.2.2.1　第一种类型:基于成分自变量的回归分析模型

1984年Aitchison等提出了对数对比模型[69],这个模型是文献[70,71]中模型的改进。线性和二次对数对比模型的形式分别为

其中y∈ℝ为实数因变量,x＝(x 1,x 2,…,x D)T∈S D为成分自变量,ε∈ℝ为随机误差项,βi为参数且满足＝0。参数可以通过最小二乘法估计,估计的参数需满足约束 ＝0。二次对数对比模型中参数众多,这将会导致数值计算困难,而且参数不好解释。

2012年Hron等提出了线性回归模型[72]。首先得出成分自变量x∈S D的ilr坐标z＝(z 1,z 2,…,z D－1)T,然后建立因变量y与自变量z的线性回归模型

y＝β0＋β1z 1＋β2z 2＋…＋βD－1z D－1＋ε

其中βi为参数,可以通过最小二乘法来估计。为了使参数的解释有意义,选用的ilr坐标形式见公式(2.2.5),第一个坐标反映的是成分x 1的相对信息,因此参数β1解释了成分x 1的相对信息对y的影响。为了得到其余成分对y的影响,可以通过对x的成分进行置换得到x(l),对应的ilr坐标为建立y与z(l)的线性回归模型

无论l的取值为多少,截距项β0都是不变的。参数β(l)1解释了成分x l的相对信息对y的影响。

2014年Lin等建立了高维成分自变量的回归模型,并提出了变量选择方法[73]。线性对数对比模型的形式为

y i＝β1 ln x i 1＋β2 ln x i 2＋…＋βD ln x iD＋εi,i＝1,2,…,n

其中βj为参数且满足＝0。由于变量经过中心化处理,所以上面模型中没有截距项。当成分数据为高维时,即D很大时,参数不能用最小二乘法进行估计,Lin等提出用l 1正则化方法来估计参数。考虑有约束的凸优化问题

其中β＝(β1,β2,…,βD)T,λ＞0为正则化参数,‖·‖1为l 1范数。运用坐标下降法来求解有约束的凸优化问题,得到参数估计^β,且^β有很好的理论性质。

2015年Marzio等针对基于成分自变量的回归分析提出了非参数回归模型[74],其形式为

y i＝f(x i)＋εi,i＝1,2,…,n

其中y i∈ℝ为因变量,x i∈S D为自变量。基于核回归方法可以得到f(x)的局部常数估计为

其中K H(·)为单形上的核函数。

2015年、2016年Bruno等[75,76]继续研究文献[74]中的模型

y i＝f(x i)＋εi,i＝1,2,…,n

基于贝叶斯P样条,可以得到

f(x i)＝B(x i)γ

其中B(x i)是n×q基矩阵B中的第i行,γ是样条系数的q维向量。基矩阵B可以通过边缘基矩阵B 1,B 2,…,B D－1得到

B＝B D－1□B D－2□…□B 1

其中B j(j＝1,2,…,D－1)的维数是n×q j,□为框积运算。例如

其中1q 2为q 2维的元素全为1的列向量,⊗为克罗克内积,·为矩阵中对应元素相乘。样条系数γ可以通过高斯马尔可夫随机场先验信息得到

γ～IGMRF q(τγ,Kγ),τγ～Gamma(a,b)

其中Kγ为系数结构矩阵,

1.2.2.2　第二种类型:基于成分因变量的回归分析模型

2008年Gueorguieva等提出了狄氏成分回归[77]。回归模型中因变量y＝(y 1,y 2,…,y D)T∈S D为成分数据,自变量x＝(x 1,x 2,…,x p)T∈ℝp为实数数据。成分因变量y的分布为狄氏分布,密度函数为

其中αj＞0(j＝1,2,…,D)为参数。每个成分y j的期望值为(www.daowen.com)

每个参数αj与自变量x之间使用ln连接函数,

其中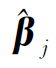是回归系数。通过最大似然法,可以得到估计后的回归系数为^βj,则参数αj对应的估计为

因此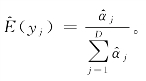狄氏成分回归可以在R软件中用程序包Dirichlet Reg来实现。

2010年Tolosana-Delgado等提出了成分多元线性回归模型[78],其形式为

y＝β0⊕x 1⊙β1⊕x 2⊙β2⊕…⊕x p⊙βp⊕ε

其中y∈S D为成分因变量,x 1,x 2,…,x p∈ℝ为p个自变量,ε∈S D为成分随机误差项,β0,β1,β2,…,βp∈S D为参数。2012年Egozcue等对上面的回归模型做ilr变换[79],得到

ilr(y)＝ilr(β0)＋x 1 ilr(β1)＋x 2 ilr(β2)＋…＋x p ilr(βp)＋ilr(ε)

首先在实数空间上获得ilr(β0),ilr(β1),ilr(β2)…,ilr(βp)的估计,然后基于ilr逆变换来获得参数β0,β1,β2,…,βp的估计。

2011年Scealy等基于超球面上的分布建立回归模型[80]。记y＝(y 1,y 2,…,y D)T∈S D为成分因变量,x＝(x 1,x 2,…,x p)T∈ℝp由p个实数自变量组成。给定z＝(z 1,z 2,…,z D)T,其中|z j|＝y j(j＝1,2,…,D)。假定z在自变量x给定下服从Kent分布,密度函数为f(z|x)＝c(k,β)－1 exp(kμ(x)T z＋β2(γ2(x)T z)2＋…＋βD－1(γD－1(x)T z)2－(β2＋…＋βD－1)(γD(x)T z)2),其中μ(x)∈S D是均值方向,γ2(x),…,γD(x)为正交的D维向量,且与μ(x)正交,k＞0,β＝(β2,…,βD－1)∈ℝD－2是形状参数,且满足

c(k,β)为归一化常数。令Γ(x)＝(μ(x),γ2(x),…,γD(x))＝H(x)K,文中给出

其中μL(x)＝(μ2(x),μ3(x),…,μD(x))T,

参数K*可以通过平面旋转矩阵得到[81]。

2015年Marzio等针对基于成分因变量的回归分析提出了非参数回归模型[74],其形式为

y i＝f(x i)⊕εi,i＝1,2,…,n,

其中y i∈S D为成分因变量,x i∈ℝp由p个实数自变量组成,εi∈S D为成分随机误差项。f(x)∈S D的局部常数估计为

其中L H(·)＝|H|－1 L(H－1·),L(·)为ℝp上的多元核函数,H是一个p×p的正定光滑矩阵[82]。根据ilr变换的等距性,f(x)∈S D的局部常数估计也可以通过下面的目标优化来求解:

同样,文中也给出了f(x)∈S D的局部线性估计。

1.2.2.3　第三种类型:基于成分因变量和成分自变量的回归分析模型

2013年Wang等基于成分因变量和成分自变量的回归分析提出了非参数回归模型[83],一个是建立在单形上,另一个是建立在实数空间上。具体形式为

y＝β1⊙x 1⊕β2⊙x 2⊕…⊕βp⊙x p⊕ε

ilr(y)＝β1 ilr(x 1)＋β2 ilr(x 2)＋…＋βp ilr(x p)＋ilr(ε)

其中y∈S D为成分因变量,x 1,x 2,…,x p∈S D为成分自变量,ε∈S D为成分随机误差项。文中给出了参数的最小二乘估计,并验证了单形上的参数估计和实数空间上的参数估计是相同的。

2015年Marzio等提出了一种基于核函数的回归模型[74],其形式为

其中y i∈S D为成分因变量,x i∈S L为成分自变量,εi∈S D为成分随机误差项。f(x)∈S D的局部常数估计为

其中K H(·)为单形上的核函数

(·)为ℝL－1上的多元核函数[82,84],H是一个(L－1)×(L－1)的正定光滑矩阵。根据ilr变换的等距性,f(x)∈S D的局部常数估计也可以通过下面的目标优化来求解

除此之外,文中还给出了f(x)∈S D的局部线性估计。