当成分数据中有零值时,对数比率变换将失效,因此在成分数据分析前需对零值进行处理。2007年Wang等提出了球坐标变换[53],该方法可以预测含有零成分的成分数据。但是当一个成分取值为1,其余成分取值都为0时,该方法失效。2008年Butler和Glasbey提出了潜高斯模型,该模型假定零值是从潜多元正态分布产生的删失观测值,但是它不能满足成分数据分析的尺度不变性和子成分一致性两个原则[54]。

近似零值、计数零值和真实零值经常出现在成分数据中[55]。由于仪器测量精度受限,低于某个临界值的数据因观测不到而记为零,这样的零值称为近似零值。近似零值不是真正的零值。例如,因为仪器受限,岩石中的某个化学成分有可能观测不到而记为零,此时的零值为近似零值。计数零值指的是当样本量不大时计数数据中未观测到的正实数值,当改变抽样设计,增加样本容量时,未观测到的数有可能会被观测到。例如,在某个时间段内某个成分的计数数据为零,但延长时间时这个成分的计数数据不为零,因此在计数数据中的零值为计数零值。真实零值是真正的零值,不是由于试验设计观测不到而记为零,即不同于近似零值。例如,滴酒不沾的家庭不会有烟酒的支出,在烟酒成分上对应的零值为真实零值。对于近似零值和计数零值,都可以用一个小的非零值来替换零值,但对于真实零值,这样替换是不合适的。下面分别介绍每种零值对应的处理方法。

1.2.1.1　近似零值

考虑成分数据集

数据集X中每一行为一个成分数据,且含有D个部分。假定成分数据中有近似零值,近似零值是由于小于已知的探测范围而观测不到所产生的,且不同成分数据相同部分对应的探测范围是相同的。记探测范围向量为e＝(e 1,e 2,…,e D)T,其中e j为成分数据集X的第j个部分对应的探测范围。

2003年Martín-Fernández等提出了乘法简单替换法[56],x ij替换后的数据为

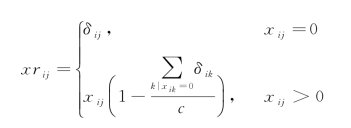
其中c为成分数据的常数和约束,即＝c,δij为一个小于e j的数。通过实验发现,当成分数据集中近似零值比例不高时,δij等于探测范围的65%时可以最小化协方差矩阵的扭曲,即δij＝65%e j。

2007年、2008年Palarea-Albaladejo等提出了一种基于alr坐标的EM算法[57,58]。记Y＝[y ij]n×(D－1)为成分数据集X通过alr变换后得到的数据集,其中Y的每一行为X的每一行对应的alr坐标。成分数据集中的近似零值x ij＜e j将会导致它对应的alr坐标y ij＜ψij,其中ψij＝近似零值x ij对应的alr坐标y ij可以当做小于某个临界值ψij的缺失数据。首先用乘法简单替换法对近似零值x ij进行初始插补,其次用EM算法对缺失数据y ij进行插补,最后通过alr逆变换得到近似零值x ij的插补值。一直这样迭代进行,直到满足某个停止准则。该方法假定alr坐标服从正态分布,第t次迭代中y ij的插补值为

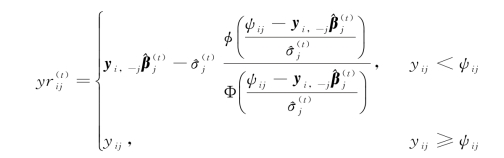
其中y i,－j为数据集Y的第i行中除了第j列的其余列,为第t次迭代中Y的第j列与其余列建立线性回归的回归系数,为第t次迭代中Y的第j列的估计的条件标准差,N(0,1)的分布和密度函数分别记为Φ(·)和φ(·)。

2012年Martín-Fernández等提出了一种基于ilr坐标的EM算法[59]。记为置换后的成分数据集,即将X的第l列置换到第1列,其余列往后移。对成分数据集X(l)做ilr变换,对应的ilr坐标为Z(l)＝首先用乘法简单替换法对X中近似零值进行初始插补。假定X(l)中第1列有近似零值,＜e l将会导致它对应的ilr坐标其中

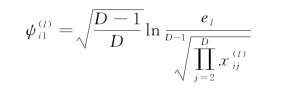
类似于上面EM算法,的插补值为

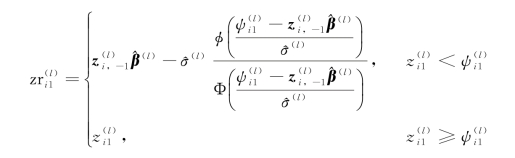
其中为数据集Z(l)的第i行中除了第1列的其余列的第1列与其余列建立线性回归的回归系数,^σ(l)为Z(l)的第1列的估计的条件标准差。将插补后的数据集取ilr逆变换可以得到近似零值的替换值。令l分别等于数据集X中近似零值对应的列指标,用上面的方法一直迭代进行,直到满足停止准则。

2013年Palarea-Albaladejo等提出了乘法对数正态替换方法[60]。该方法假定成分数据集中的每个成分服从对数正态分布ln x j～N(μj,第j个成分的近似零值x ij＜e j会导致ln x ij＜ln e j。首先对ln x ij进行插补,使得插补后的值小于ln e j,然后取指数得到近似零值x ij的替换值,具体公式为分别为μj,σj的估计值。

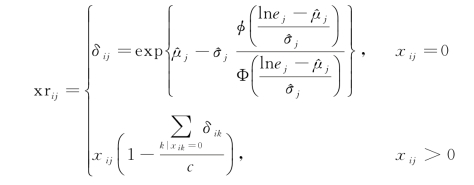
2014年Palarea-Albaladejo等提出了一种基于alr坐标的数据扩充算法[61]。该方法与基于alr坐标的EM算法非常相似,区别在于EM算法的更新是确切的,而该方法的更新是通过模拟得到的。给定参数估计^μ,^Σ,当y ij＜ψij时,y ij的插补值yr ij是通过概率分布P(y ij|

其中模拟得到的,新的参数估计值^μ,^Σ是通过概率分布P(μ,Σ|yr ij,y i,－j)模拟得到的。

2015年Palarea-Albaladejo等又提出了Kaplan-Meier平滑样条替换方法[62]。该方法是一种非参数方法,经常被用在生存分析中。通过经验累积分布函数(ECDF)来对近似零值进行插补,具体公式为

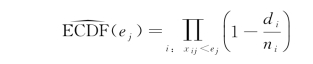
其中d i和n i分别为在时间i观测到的事件个数和总事件个数。

2016年Templz等针对高维成分数据中的近似零值,提出了一种基于ilr坐标的偏最小二乘回归插补法[63]。该方法与基于ilr坐标的EM算法非常相似,之前的方法中回归系数是通过线性回归分析得到的,而该方法中回归系数是通过偏最小二乘回归分析得到的,其余步骤保持不变。

以上介绍的所有近似零值插补方法都可以在R软件中用程序包zCompositions中的函数cmult Repl,lr EM,mult LN,lr DA,mult KM来实现。

1.2.1.2　计数零值

2015年Martín-Fernández等针对计数零值提出了贝叶斯乘法替换方法[64]。该方法是贝叶斯方法和乘法简单替换法的结合。首先用贝叶斯方法对零值和非零成分进行后验估计,然后利用乘法简单替换法进行修正,使得原始非零成分之间的比率保持不变。具体过程如下:

考虑计数向量c＝(c 1,c 2,…,c D)T,它服从多项式分布,分布中的概率为θ＝(θ1,θ2,…,θD)T。θ的先验分布为关于参数向量α＝(α1,α2,…,αD)T的狄氏先验分布,其中αj＝sp j(j＝1,2,…,D),s为先验的强度。向量p＝(p 1,p 2,…,p D)T为θ的先验期望,因此 ＝1。当向量c的取值给定后,根据贝叶斯定理,θj的后验估计为

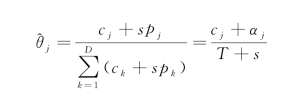(www.daowen.com)

其中T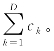＝对于固定的T,几乎所有被提出来的狄氏先验分布都是对称的,因此p为均匀向量(1/D,1/D,…,1/D)T。不同的狄氏先验分布对应不同的强度s,相应的后验估计见表1.2.1。

表1.2.1　不同狄氏先验分布下的后验估计

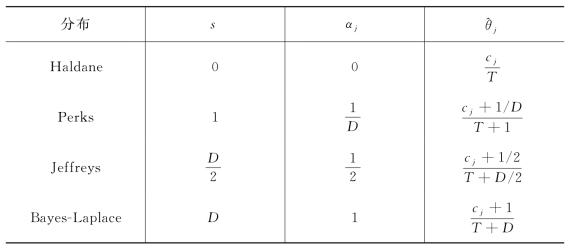
上面给出的贝叶斯方法可以对计数数据进行修正,但是非零成分的比率有可能发生变化。例如,考虑计数向量c＝(4,0,2)T,则T＝6,D＝3,第一个成分与第三个成分之间的比率为2。成分数据x＝(2/3,0,1/3)T的贝叶斯估计为

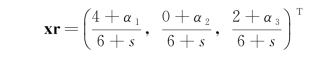
贝叶斯估计中第一个成分与第三个成分的比率为当狄氏先验分布为Haldane时,2,虽然非零成分的比率没变,但此时零成分依然还是零值。当狄氏先验分布为其他先验分布时,因此需对通过贝叶斯方法得到的估计值进行调整,使得非零成分之间的比率不变。基于乘法简单替换法调整后,通过贝叶斯乘法替换法得到的估计值为

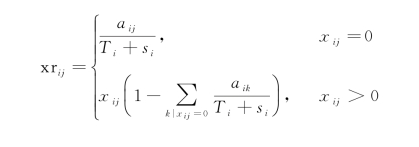
接着上面例子,成分数据x的贝叶斯乘法替换估计为

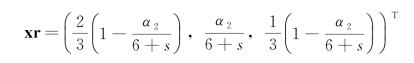
很显然可以看出通过贝叶斯乘法替换法得到的第一个成分与第三个成分之间的比率为2。为了使总计数T＝6不变,可以对xr乘以6,从而得到

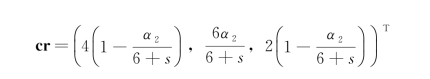
为了使非零成分分别为原始成分,可以对xr乘以6/(1－从而得到

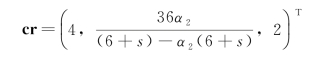
当狄氏先验分布的α2和s值给定后,我们可以计算出cr。

上面介绍的贝叶斯乘法替换方法可以在R软件中用程序包zCompositions中的函数cmult Repl来实现。

1.2.1.3　真实零值

1986年Aitchison提出了通过合并成分部分来处理真实零值[19],把零成分与非零成分合并为一个非零成分。虽然成分合并可以减少零值的数量,但它关于Aitchison几何是一种非线性运算,而且丢失了对应成分部分比率间的信息。

2003年Aitchison等提出了处理真实零值的参数方法[65]。通过两阶段来建立模型:第一阶段是决定零值出现的位置,第二阶段是给出非零部分对应的子成分的分布。考虑成分数据x∈S D,假定x中有真实零值。给定变量u＝(u 1,u 2,…,u D)T,其中u j(j＝1,2,…,D)为二元变量0或1,u j＝0代表x的第j个成分为真实零值,u j＝1代表x的第j个成分为一个正实数。

第一阶段是给出变量u的密度函数。假定每个二元变量u j成功的概率为θj。独立二项模型中u的密度函数为

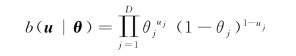
独立二项模型的不足是没有考虑D个二元变量u j的相依性,因此增加先验信息(j＝1,2,…,D)。相依二项模型中u的密度函数为

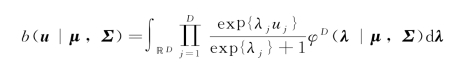
其中λ＝(λ1,λ2,…,λD)T服从正态分布,密度函数为φD(λ|μ,Σ),μ,Σ分别为期望和协方差阵。

第二阶段是给出成分数据x中非零成分对应的子成分的密度函数。假定成分数据x服从logistic正态分布,密度函数为ψ(x|ξ,T),其中ξ为成分数据的中心,T为成分数据的方差矩阵。记J(u)＝{j:u j＝1},K(u)＝{j:u j＝0},J(u)为成分数据x的非零成分对应的部分指标集,K(u)为成分数据x的真实零值对应的部分指标集。非零成分对应的子成分x J(u)服从正态分布,密度函数为ψ(x J(u)|ξJ(u),T J(u)),其中ξJ(u),T J(u)分别为ξ,T中指标集J(u)对应的向量和矩阵。给定n个成分数据样本点,第i个样本点对应的二元变量为u i＝(u i 1,u i 2,…,u iD)T,非零成分对应的子成分为x J(u i)。独立二项条件logistic正态模型对应的似然函数为

相依二项条件logistic正态模型的似然函数为

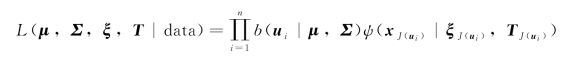
通过似然函数极大化可以求出参数θ,ξ,T或μ,Σ,ξ,T的估计。

之后提出的方法都是在上面参数方法的基础上进行改进的。2011年Stewart等在进行定量脂肪酸特征分析时,针对真实零值提出了混合模型,并给出了模型的推论[66]。2016年Bear等提出了对数正态混合模型,将对数正态分布推广为不同维数的对数正态分布的混合,并通过似然方法给出了参数的估计[67]。2017年Templ等针对有真实零值的成分数据,提出了一种异常值检测的方法,该方法是通过估计子成分间的马氏距离来检测的[68]。