水质分析中所得到的许多物理、化学和生物学数据，是描述和评价环境质量的基本依据。由于监测系统的条件限制以及操作人员的技术水平，测试值与真值之间常存在差异；环境污染的流动性、变异性以及与时空因素关系，使某一区域的环境质量由许多因素综合所决定；描述某一河流的环境质量，必须对整条河流按规定布点，以一定频率测定，根据大量数据综合才能表述它的环境质量，所有这一切均需通过统计处理。

一、数据的处理和结果表述

1. 数据修约规则

各种测量、计算的数据需要修约时，应遵守下列规则：四舍六入五考虑，五后非零则进一，五后皆零视奇偶，五前为偶应舍去，五前为奇则进一。

[例1-1]　将下列数据修约到只保留一位小数：14.342 6、14.263 1、14.250 1、14.250 0、14.050 0、14.150 0

解：按照上述修约规则

表2-14　数据修约前后一览表

解析：

（1）修约前修约后因保留一位小数，而小数点后第二位数小于、等于4者应予舍弃。

（2）小数点后第二位数字大于或等于6，应予进一。

（3）小数点后第二位数字为5，但5的右面并非全部为零，则进一。

（4）小数点后第二位数字为5，其右面皆为零，则视左面一位数字，若为偶数（包括零）则不进，若为奇数则进一。若拟舍弃的数字为两位以上数字，应按规则一次修约，不得连续多次修约。

[例1-2]　将15.454 6修约成整数

表2-15　数据修约前后比较

2. 可疑数据的取舍

与正常数据不是来自同一分布总体、明显歪曲实验结果的测量数据，称为离群数据。可能会歪曲实验结果，但尚未经检验断定其是离群数据的测量数据，称为可疑数据。

在数据处理时，必须剔除离群数据以使测量结果更符合客观实际。正确数据总有一定的分散性，如果人为地删去一些误差较大但并非离群的测量数据，由此得到精密度的测量结果并不符合客观实际。因此对可疑数据的取舍必须遵循一定的原则。

测量中若发现明显的系统误差和过失，则由此产生的数据应随时剔除。而可疑数据的取舍应采用系统方法判别，即离群数据的统计检验。检验的方法很多，现介绍最常用的两种。

（1）狄克松（Dixon）检验法

此法适用于一组测量值的一致性检验和剔除离群值，本法中对最小可疑值和最大可疑值进行检验的公式因样本容量（n）不同而异，检验方法如下：

①将一组测量数据按从小到大顺序排列为x1、x2…xn，x1和xn分别为最小可疑值和最大可疑值。

②按表2-16计算式求Q值。

③根据给定的显著性水平（α）和样本容量（n），从表2-17查的临界值（Qα）。

④若Q≤Q0.05，则可疑值为正常值；若Q0.05≤Q≤Q0.01，则可疑值为偏离值；若Q＞Q0.01，则可疑值为离群值。

表2-16　狄克松检验法Q值积算式

续表

表2-17　狄克松检验法临界值（Q）

[例1-3]　一组测量值从大到小顺序排列为：14.65、14.90、14.90、14.92、14.95、14.96、15.00、15.01、15.01、15.02。检验最小值14.65和最大值15.02是否为离群值。

解：检验最小值x1=14.65，n=10，x2 =14.90，xn-1=15.01，则：

查表2-16，当n=10，给定显著性水平α=0.01时，Q0.01=0.597。

Q＞Q0.01，故最小值14.65为离群值，应予剔除。

检验最大值xn=15.02，有：

查表2-17可知，Q0.05=0.477。

Q＜Q0.05，故最大值15.02为正常值。

（2）格鲁布斯（Grubbs）检验法

此法适用于检验多组测量值均值的一致性和剔除多组测量值中的离群均值；也可用于检验一组测量值的一致性和剔除一组测量值中的离群值，方法如下：

①有l组测量值，每组n个测量值的均值分别为，其中最大均值记为，最小均值记为。

②由l个均值计算总均值（）和标准偏差（）：

③可疑均值为最大均值（）时，按下式计算统计量（T）：

可疑均值为最小值（）时，按下式计算统计量（T）：

④根据测量值组数和给定的显著性水平（α），从表2-18查得临界值（Tα）。

⑤若T≤T0.05，则可疑均值为正常均值；若T0.05＜T≤T0.01，则可疑均值为偏离均值；若T＞T0.01，则可疑均值为离群均值，应予剔除，即剔除含有该均值的一组数据。

表2-18　格鲁布斯检验法临界值（Tα）

3. 监测结果的表述

对一个样品某一指标的测定，其结果表达方式一般有如下几种：

①用算术平均值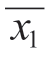（）表示测量结果与真值的几种趋势

测量过程中排除系统误差和过失后，只存在随机误差，根据正态分布的原理，当测定次数无限多（n→∞）时的总体均值（u）应与真值（）很接近，但实际测量次数有限。因此样本的算术平均值是表示测量结果与真值的集中趋势以表达监测结果的最常用的方式。

②用算术平均值和标准偏差表示测量结果的精密度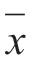（±S）

算术平均值代表集中趋势，标准偏差表示离散程度。算术平均值代表性的大小与标准偏差的大小有关，即标准偏差大，算术平均值代表性小，反之依然，故而检测结果常以（±S）表示。

③用表示结果

标准偏差大小还与所测均值水平或测量单位有关。不同水平或单位的测量结果之间，其标准偏差是无法进行比较的，而变异系数是相对值，故可在一定范围内用来比较不同水平或单位测量结果之间的差异。例如：镉试剂分光光度法测量镉，当镉质量浓度小宇0.1 mg/L时，标准偏差和变异系数分别为7.3%和9.0%。

二、误差和偏差

1.真值（xt）

在某一时刻和某一位置或状态下，某量的效应体现出客观值或实际值称为真值。真值包括：

（1）理论真值：例如三角形内角之和等于180°；

（2）约定真值：由国际计量大会定义的国际单位制，包括基本单位、辅助单位和导出单位。由国际单位制所定义的真值叫约定真值；

（3）标准器（包括标准物质）的相对真值：高一级标准器的误差为低一级标准器或普通仪器误差的1/5（或1/3～1/20）时，则可认为前者是后者的相对真值。

2.误差及其分类

由于被测量的数据形式通常不能以有限位数表示，同时由于认识能力不足和科学技术水平的限制，使测量值与真值不一致，这种矛盾在数值上表现即为误差。任何测量结果都有误差，并存在于一切测量全过程之中。误差按其性质和产生原因，可分为系统误差、随机误差和过失误差。

（1）系统误差：又称可测误差、恒定误差或偏倚（bias）。指测量值的总体均值与真值之间的差别，是由测量过程中某些恒定因素造成的，在一定条件下具有重现性，并不因增加测量次数而减少系统误差，它的产生可以是方法、仪器、试剂、恒定的操作人员和恒定的环境所造成。

（2）随机误差：又称偶然误差或不可测误差。是由测定过程中各种随机因素的共同作用所造成，随机误差遵从正态分布规律。

（3）过失误差：又称粗差。是由测量过程中犯了不应有的错误所造成，它明显地歪曲测量结果，因而一经发现必须及时改正。

（4）误差的表示方法：分绝对误差和相对误差。绝对误差是测量值（x，单一测量值或多次测量的均值）与真值（xt）之差，绝对值有正负之分。

式中　x——单一测量值或多次测量值的均值；

xt——真值；

A——绝对误差；

相对误差指绝对误差与真值之比（常以百分数表示）：

式中　A——绝对误差；

B——相对误差；

Xt——真值；

3.偏差

相对偏差、平均偏差、相对平均偏差和标准偏差等。

（1）绝对偏差（di）是测定值与均值之差，即(www.daowen.com)

式中　di——绝对偏差；

xi——测定值；

——均值；

（2）相对偏差是绝对偏差与均值之比（常以百分数表示）：

式中　bi——相对偏差；

di——绝对偏差；

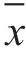——均值；

（3）平均偏差是绝对偏差绝对值之和的平均值：

式中　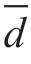——平均偏差；

di——绝对偏差，其中（i=1、2…n）；

（4）相对平均偏差是平均偏差与均值之比（常以百分数表示）：

式中　M——相对平均偏差；

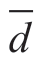——平均偏差；

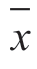——均值；

4.标准偏差和相对标准偏差

（1）差方和：亦称离差平方或平方和。是指绝对偏差的平方之和，以S表示：

（2）样本方差用s2或V表示：

（3）样本标准偏差用s或sD表示：

（4）样本相对标准偏差：又称变异系数，是样本标准偏差在样本均值中所占的百分数，记为Cv。

（5）总体方差和总体标准偏差分别以σ2和σ表示：

式中　N——总体容量；

μ——总体均值。

（6）极差：一组测量值中最大值（Xmax）与最小值（Xmin）之差，表示误差的范围，以R表示R=Xmax-Xmin

5. 总体和个体

研究对象的全体称为总体，其中一个单位叫个体。

6. 样本和样本容量

总体中的一部分叫样本，样本中含有个体的数目叫此样本的容量，记作n。

7. 平均数

平均数代表一组变量的平均水平或集中趋势，样本观测中大多数测量值靠近

（1）算术均数：简称均数，最常用的平均数，其定义为：

（2）几何均数：当变量呈等比关系，常需用几何均数，其定义为：

（3）中位数：将各数据按大小顺序排列，位于中间的数据即为中位数，若为偶数取中间两数的平均值，适用于一组数据的少数呈“偏态”分散在某一侧，使均数受个别极数的影响较大。

（4）众数：一组数据中出现次数最多的一个数据。

平均数表示集中趋势，当监测数据是正态分布时，其算术均数、中位数和众数三者重合。

三、正态分布

相同条件下对同一样品测定中的随机误差，均遵从正态分布。正态概率密度函数为：

式中　x——由此分布中抽出的随机样本值；

μ——总体均值，是曲线最高点的横坐标，曲线对μ对称；

σ——总体标准偏差，反映了数据的离散程度。

从统计学知道，样本落在下列区间内的概率如表2-19所示。

表2-19　正态分布总体的样本落在下列区间内的概率

实际工作中，有些数据本身不呈正态分布，但将数据通过数学转换后可显示正态分布，最常用的转换方式是将数据取对数。若监测数据的对数呈正态分布，称为对数正态分布。例如，大气监测当SO2成颗粒物浓度较低时，数据经实验证明一般呈对数的正态分布，有些工厂排放废水的浓度数据也呈对数正态分布。差别无显著意义，即两种分析方法的可比性很好。

四、直线相关和回归

在环境监测中经常要了解各种参数之间是否有联系，例如，BOD和TOC都是代表水中有机污染的综合指标，它们之间是否有关？又如在水稻田施农药，水稻叶上农药残留量与施药后天数之间是否有关？下面将介绍怎样判断各参数之间的联系。

1.相关和直线回归方程

变量之间关系有两种主要类型：

（1）确定性关系

例如欧姆定律V=IR，已知三个变量中任意两个就能按公式求第三个量。

（2）相关关系

有些变量之间既有关系又无确定性关系，称为相关关系，它们之间的关系式叫回归方程式，最简单的直线回归方程为：

式中a、b为常数，当x为x1时，实际y值在按计算所得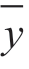左右波动。

上述回归方程可根据最小二乘法来建立。即首先测定一系列x1、x2…xn和相对应的y1、y2…yn，然后按下式求常数a和b。

2.相关系数及其显著性检验

相关系数是表示两个变量之间关系的性质和密切程度的指标，符号为v，其值在-1—+1之间。公式为：

x与y的相关关系有如下几种情况：

（1）若x增大，y也相应增大，称x与y呈正相关。此时0＜v＜1，若v=1，称完全正相关。

（2）若x增大，y相应减小，称x与y呈负相关。此时，-1＜v＜0，当v=-1时，称完全负相关。

（3）若y与x的变化无关，称x与y不相关。此时v=0。

若总体中x与y不相关，在抽样时由于偶然误差，可能计算所得v≠0。所以应检验v值有无显著意义，方法如下：

①求出v值。

②按求出，求出t值，n为变量配对数，自由度n1=n-2

③查t值表（一般单侧检验）。

若t＞t0.01（n） P＜0.01v有非常显著意义而相关；

若t＜t0.1（n） P＞0.1v关系不显著。

[例1-4]　用Ag-DDC法测砷时得到下表所列数据。求其线性关系如何，并作显著性检验。

解：∑x=29.50 ∑y=0.874

从v=0.999 3可知x与y几乎成完全正相关。

显著性检验：

因本例是正相关，不会出现负相关，用单侧检验，查表得t0.01（6）单侧=3.14

t=65.42＞＞3.14＝t0.01（6）

所以相关有非常显著意义。