工程上是用含沙浓度 （S）表示水流中沙量的多少。含沙浓度常用下面三种表示方法：

上面三种浓度之间存在如下关系：

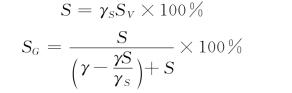
1.劳斯泥沙浓度分布

下面我们根据紊流扩散理论推求含沙浓度在铅垂线上分布的表达式。如图14.5.1所示，给出了恒定二元浑水中某铅垂线上时均含沙浓度分布及时均流速分布。在此铅垂线上取一与流向平行的单位面积a，此处的含沙浓度为S，则在重力作用下，由于沉速ω在单位时间内通过单位横截面积a下沉的悬移质数量为：

又由于紊动作用泥沙从下层向上层扩散现象与液体的分子扩散现象相类似，两者规律相同。分子扩散理论的费克（A.Fick）第一定律为：

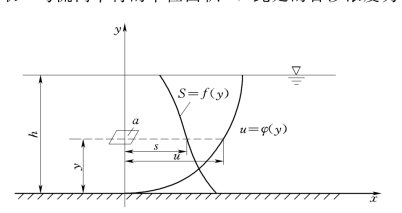
图14.5.1

式中 c——扩散物质的质量浓度，量纲为M/L 3；

Dm——扩散物质在水中的扩散系数，量纲为L 2/T；

F——单位时间内，通过垂直于n方向的单位面积的扩散物质量，称为扩散物质输送率，量纲为M/T/L 2。

式 （14.5.2）说明：扩散物质在某个方向上的输送率与该方向上的浓度梯度成正比。式中的负号表示物质的扩散方向与浓度增加方向相反。

将费克第一定律应用于泥沙扩散问题，则有：

式中 εs——悬移质的扩散系数；

d S/d y——含沙浓度梯度；

q2——由于紊动扩散作用单位时间内通过单位横截面积a上升的泥沙量。

在不冲不淤的相对平衡状态下，重力使泥沙下沉的沙量q1应该等于紊动使泥沙向上层扩散的沙量q2，于是得：

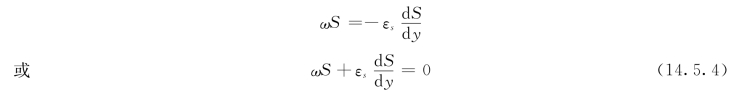
下面我们确定泥沙的扩散系数εs。我们是将紊流中的泥沙扩散现象同紊流中的动量交换（扩散）现象进行比较来确定泥沙的扩散系数εs的。描述两种现象的公式分别为：

(www.daowen.com)

式 （14.5.3）表示具有不同含沙量的涡体因紊动混掺进行泥沙交换从而在单位截面积上产生泥沙扩散现象。式 （14.5.4）表示具有不同动量的涡体因紊动混掺进行动量交换，从而在单位截面积上产生紊流附加切应力。式中S是单位浑水中的含沙量，而ρu是单位水流体积中具有的动量。εs是泥沙的扩散系数，ε是紊动运动黏度。从上述对比中可以看出：这两种现象是极其相似的，因此式中的系数εs同ε也是极其相似的，它们都是紊动涡体所含的特征量泥沙或动量的扩散系数，故劳斯（Rouse）假设εs=ε。

由式（14.5.4）得：

又对于如图14.5.2所示的二元水流，因为流速u只是水深y的函数，所以认为在边壁ac和bd上不存在切应力，只在ef和cd周界上存在切应力。故图中abfe的水力半径为：

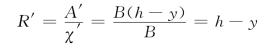
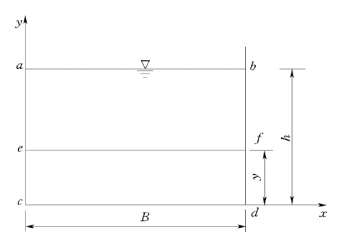
图14.5.2

而abdc的水力半径为R=A/X=Bh/B=h。所以ef和cd边壁上的切应力τ和τ0分别为：

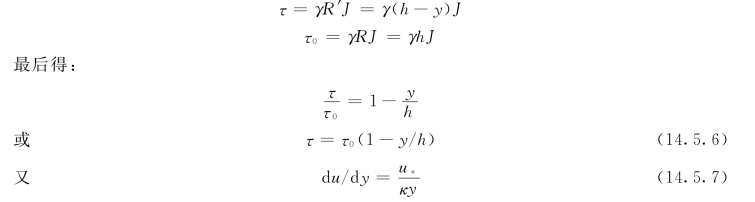
将式（14.5.6）、式 （14.5.7）代入式（14.5.5），并注意到τ0/ρ=u 2*，则得：

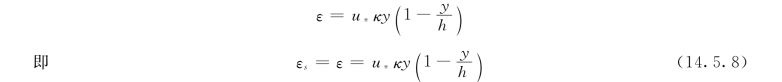
将式（14.5.8）代入式（14.5.4），得：

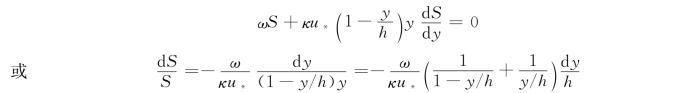
将上式从a到y的范围内积分，并令Sa为y=a处的时均含沙浓度，也称为基点浓度，一般取a=0.05h，h为渠中水深，积分得：

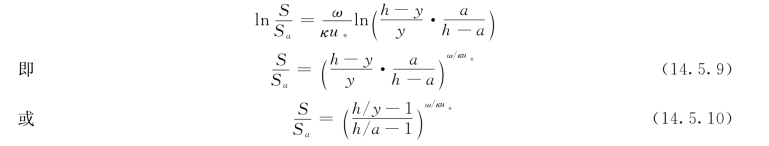
式 （14.5.9）、式 （14.5.10）就是二元恒定均匀流在平衡输沙时含沙浓度沿铅垂线的分布公式，也称为劳斯分布式。式中指数z=ω/ （кu*）称为悬浮指数，它表示重力作用与紊动作用的相对关系。重力作用由ω表示，紊动作用由кu*表示。z愈大表明重力作用愈强，因而含沙浓度沿铅垂线分布愈不均匀；反之如果z愈小，则表明紊动作用强，因而分布就愈均匀。图14.5.3给出了不同z值时由式 （14.5.6）画出的泥沙沿铅垂线的分布曲线。从图中看出：当泥沙颗粒大到使z≥1.5时泥沙就悬浮不到水面；当z≥5以后，悬浮形式运动的泥沙微乎其微，因此以z=5作为泥沙是否进入悬浮状态的判别标准。

2.莱恩—卡林斯基泥沙浓度分布

泥沙的扩散系数εs沿水深h是变化的，而莱恩—卡林斯基（Lane Kalinske）是取水深h上的平均泥沙扩散系数εm代替变化的εs，并令к=0.4，由式（14.5.8）得：

将式（14.5.11）代入式（14.5.4）积分，积分限仍然是a到h，且y=a时S=Sa，于是得：

式 （14.5.12）称为莱恩—卡林斯基泥沙浓度分布式，也称为劳斯泥沙浓度分布简式。