前面介绍的希尔兹和岩垣的临界推力公式（14.3.7）和式（14.3.8）都是对单一的等粒径泥沙而言的，而实际中河床或渠床上的泥沙是由大小不同粒径组成的混合泥沙。由于混合泥沙中的粗颗粒对细颗粒有一种遮蔽作用，因此同等粒径的均匀泥沙相比，要起动混合泥沙中相同粒径的细颗粒泥沙所需要的临界推力要大，但起动粗颗粒泥沙所需的临界推力要小，因为这时细颗粒泥沙对粗颗粒泥沙已无制约作用。

混合泥沙的临界推移力公式是由耶格阿扎罗夫（Egiazaroff）于1965年提出的。河渠中的流速分布公式为：

假设研究混合泥沙中粒径为di的沙粒，水流作用在该沙粒上的绕流阻力为RTi，表示RTi的代表流速为ubi，ubi是距河底y=aidi处的流速。又假设混合泥沙的当量粗糙度ks近似地等于平均粒径dm，这样ubi可由下式求出：

水流作用在泥沙颗粒上的绕流阻力RTi可以表示为：

河床作用在泥沙颗粒上的摩擦力Fi可以表示为：

式中 φ——泥沙的自然摩擦角。

在临界起动条件下RTi=Fi，于是得：

将式（14.3.10）代入式 （14.3.13），根据实验ai=0.63，tanφ=1，令u*=u*c，则得：

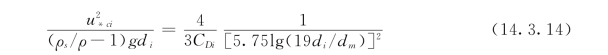
又根据实验CDi=0.4，代入上式后，得耶格阿扎罗夫公式为：

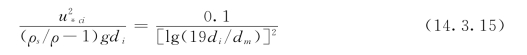
当di=dm时上式变为：

由式（14.3.15）和式（14.3.16）得：

(www.daowen.com)

式 （14.3.17）表示混合泥沙中每个粒径的临界推移力与平均粒径dm的临界推移力之比。实验资料证明：在di/dm＞0.4的范围内，上式与实验资料非常吻合，然而在di/dm≤0.4的范围内，上式与实验资料偏差较大。为此，平野、芦田、道上对di/dm≤0.4提出下式：

归纳前述，得计算混合泥沙各不同粒径临界推移力的公式为：

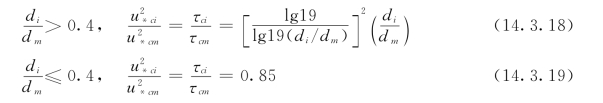
上面两式中对于平均粒径dm的临界推移力τcm可以按希尔兹公式 （14.3.7）或岩垣公式（14.3.8）计算。

例14.3.1 有一河流，构成河床泥沙的粒径范围和级配如表14.3.1中①、②栏所给，该河道中水深h=2.0m，水力坡度J=1/1500，试检查该河床中泥沙的起动情况。

解：

下面以粒径组d=0.01～0.04cm为例说明计算步骤。

1）①、②栏为已知数据。

2）③栏是各粒径组的平均粒径，这里是采用几何平均粒径，即

3）④栏是各粒径组的几何平均粒径与该粒径组泥沙重量占混合泥沙总重量百分比的乘积，由式（14.2.4）得总体平均粒径为：

表14.3.1　各种粒径泥沙临界摩阻流速的计算

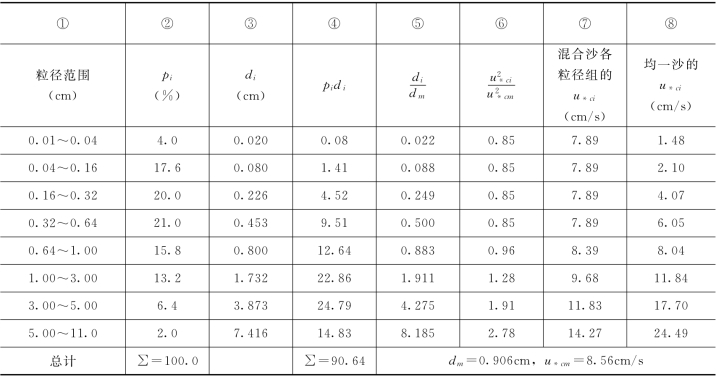
6）根据dm=0.906cm，用岩垣公式（14.3.8）先计算总体平均粒径的摩阻流速u*cm。因为dm＞0.303cm，所以

将表14.3.1第⑦栏中各粒径组的u*ci与水流摩阻流速相比较，可见在混合沙中，前6个粒径组的泥沙将被起动，后2个粒径组的泥沙则不被起动。

在⑧栏中也给出了将各粒径组作为均一泥沙时由岩垣公式算得的u*ci。以此与考虑组合粒径计算的u*ci相对照可以看出，两者的u*ci值在细粒径侧和粗粒径侧相差较大。细粒径侧混合泥沙的u*ci大，这是由于混合泥沙中的细粒径泥沙在起动时受到周围粗粒径泥沙的牵制作用的结果；粒径偏粗的混合泥沙的u*ci小，这是由于当混合泥沙中的细粒径泥沙起动后，粗粒径泥沙彼此之间很少再有牵制作用的结果。从第⑧栏中可见，作为均一泥沙，当水流的摩阻流速u*=11.43cm/s时，前5个粒径组的泥沙将被起动，后3个粒径组的泥沙则不被起动。