静水中的泥沙颗粒在重力作用下将会下沉，又在泥沙下沉的过程中将引起水流的阻力，当水中泥沙颗粒的有效重力（泥沙颗粒的干重量减去浮力）与作用在泥沙颗粒上的阻力相平衡时，泥沙颗粒将匀速下沉。我们将泥沙颗粒在静止清水中匀速下沉的速度定义为泥沙的沉降速度，记为ω，单位为cm/s。由于泥沙颗粒愈粗沉降速度愈大，即沉降速度反映了泥沙颗粒的粗细，因此泥沙的沉降速度又叫做泥沙的水力粗度。泥沙的沉降速度或水力粗度综合地反映了泥沙颗粒形状、大小、比重及水流阻力的物理量，是研究泥沙运动时经常用到的一个重要参数。

泥沙颗粒在水中的有效重力为：

泥沙颗粒在水中所受的绕流阻力，一般可以表示为：

式（12.2.6）中的CD是绕流阻力系数，它与流态有关，即与雷诺数Re=ωd/ν有关，ω、d和ν分别是沙粒的沉降速度、沙粒直径和水的运动黏度。对于圆球绕流问题，早在1851年，斯托克斯就总结出了阻力系数CD随雷诺数Re的变化规律。如图14.2.2所示。从图中可见，当雷诺数Re＜0.5时，绕流阻力系数CD呈直线变化，且随Re增大而减小，即服从斯托克斯定律，为层流绕流，即有：当雷诺数Re＞1000以后，为紊流绕流，绕流阻力系数大致可以看作为常数，其范围在0.43～0.45。在从层流向紊流绕流的过渡区，绕流阻力系数没有理论公式，一般都是实验公式，且各家不一。

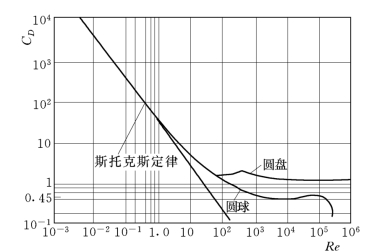
图14.2.2

根据作用在球形泥沙颗粒上的有效重力与阻力平衡可以求出泥沙颗粒的沉降速度ω。

1.层流绕流

注意到Re=ωd/ν，A=πd 2/4。先将式（14.2.7）代入式（14.2.6），然后令式（14.2.6）等于式（14.2.5），则得：

整理后得：

2.紊流绕流

首先将CD=0.45代入式（14.2.6），然后令式（14.2.6）等于式（14.2.5），得：

故

请注意：上面计算泥沙沉速的公式是对圆球状颗粒而言的。事实上，自然泥沙颗粒不可能是圆球状的，形状是不规则的。因此绕流阻力系数均比按式（14.2.7）计算的大或比0.45大，于是沉降速度较按式（14.2.9）和式（14.2.10）计算的小。

根据张瑞瑾的研究，给出下面适用于自然泥沙的沉降速度公式。(www.daowen.com)

（1）层流绕流。适用条件：Re＜0.5，常温下（15～25℃），d＜0.1mm。

（2）过渡区。适用条件：0.5＜Re＜1000。

（3）紊流绕流。适用条件：Re＞1000，常温下，d＞4mm。

事实证明：式 （14.2.12）不仅适用于过渡区，而且对层流区和紊流区均适用。因此说，式 （14.2.12）是计算自然泥沙沉降速度的一般公式。

另外，还常用鲁比（Rubey）公式计算泥沙的沉降速度，即

式中s= （γs-γ）/γ，泥沙沉速公式的单位均为cm/s。

例14.2.1 已知某标准沙的直径d=0.30mm，在水中的比重s=1.65，水温为20℃，试分别用张瑞瑾公式和鲁比公式计算该标准沙在水中的沉降速度ω。

解：

（1）张瑞瑾公式

已知该沙直径大于0.1mm，但是小于4mm，因此在沉降过程中处于过渡区，按式（14.2.12）计算。20℃时水的运动黏度ν=0.01cm2/s。式中（γs-γ）/γ=s=1.65，d=0.03cm，将这些已知数据代入式（14.2.12）得：

（2）鲁比公式

按式 （14.2.14）计算：

得

上面两式计算的结果相当一致，彼此的相对差值只有1.2%。