明渠非恒定急变流主要指非连续波区的流动。这种非恒定流的特征是波的前锋陡峻，水面不连续且常形成台阶状断波，如图13.2.9所示。断波波峰向前移动的速度称为波速，以ω1表示。断波波峰到达某断面时，立即扰动该断面的水情，使水深、流速等发生变化。从计算角度讲，波峰未到时的水流可视作未扰动的原有恒定流，波峰经过后的非恒定流主体部分则可近似地认为是明渠非恒定渐变流，波峰处则是急变流。所以水力计算的基本问题是要确定断波波速ω1与波峰处其他水力参数的关系以及波峰前水深h和流速v之间的关系。前者决定了非恒定流的影响范围，后者则是非恒定渐变流段 （非恒定流主体部分）计算时的边界条件。

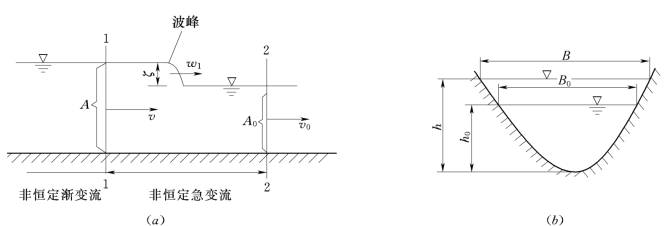
图13.2.9

计算上述问题的基本方程是在断波处（急变流段）列出的连续方程和动量方程。

取图13.2.9中1-1、2-2两断面间的空间为控制体，由第3章质量守恒式：

式中第一项为控制体内水体质量的变化率，即单位时间内控制体中水体质量的增量，故

式中ω1为断波波速，A、B和A0、B0分别为断波前后1-1、2-2断面的面积和水面宽度，ζ为断波高度。质量守恒式中第二项为单位时间内通过控制体表面的水体质量，即

式中v、v0分别为1-1、2-2断面的平均流速。

将式（13.2.37）、式 （13.2.38）代入质量守恒式得：

同时可写出断波波高的表达式为：

式中B′为平均水面宽度。

动量定律可由式（3.3.6）得出：

仍取图13.2.9中1-1、2-2两断面间的空间为控制体，列其沿水流方向的动量方程，在忽略壁面摩擦力及底坡影响时，式 （3.3.6）中左端项为：

(www.daowen.com)

式中P及P0为作用在1-1、2-2断面上的动水压力。式 （3.3.6）右端第一项为控制体内水体动量变化率，即第二项为单位时间内通过控制体表面流出流进水体所具动量之差，即

将式（13.2.41）、式 （13.2.42）、式 （13.2.43）代入式（3.3.6）得断波处动量方程：

由连续方程式（13.2.41）及动量方程式（13.2.42）经整理后可得断波波速ω1及断波前后流速和水深的关系式：

及

以上式中根号前“+”号相应于顺波情况，“-”号相应于逆波情况。由于断面面积A和动水压力P 均是水深h的函数，而A0和v0均为已知的初始值，所以式 （13.2.46）就是断波处水深和流速的关系式。

存在明渠非恒定急变流段的仍可采用有限差分法逐时段地进行计算。对每一时段，可由时段初瞬时的水力要素按断波波速公式（13.2.45）求出波速ω1并由此求小时段末瞬时的断波位置。由断波区水深和断面平均流速的关系式 （13.2.46）作为边界条件推求该时段末瞬时非恒定渐变流段（波动的主体部分）的水力要素，由此也可得出断波区的水力要素，并由此推求下一时段的断波波速。详细过程这里不再赘述，读者可参阅有关文献。

例13.2.1 有一矩形渠道，底宽B=4.0m，自闸下泄出的流量为4.4m3/s，闸下游水深为0.6m，如将闸门突然开大，流量增至6.7m3/s，试求波速ω1及波高ζ。

解：

增大的流最为：

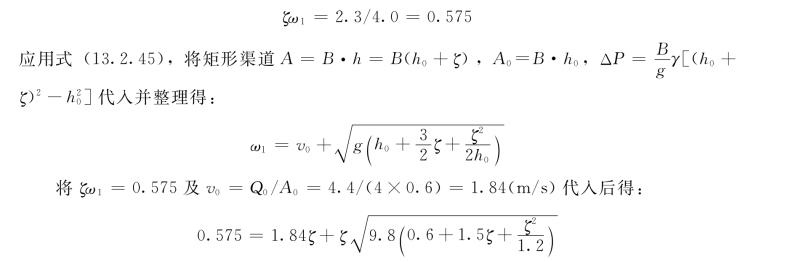
应用式（13.2.40），Q-Q0=B′ζω1，代入具体数值，得：

用试算法求得ζ=0.125m，代入ζω1=0.575中，可求出ω1=4.6m/s。