明渠非恒定渐变流的基本问题是确定水力要素如流量 （或流速）、水位 （或水深）随时间t和流程s的变化规律。求解明渠非恒定渐变流的基本方程式仍是连续方程和运动方程。

1.连续方程

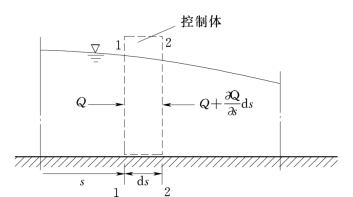
图13.2.3

在河渠中任取一微小渠段d s并以其两端过水断面1-1及2-2所围水体作控制体（即取渠底为控制体下边界，自由水面以上的空间中任取一上边界），如图13.2.3所示，根据质量守恒原理，针对此控制体列出的明渠非恒定流连续方程为第3章式（3.4.7）。

式中 Q——流量；

A——过水断面面积。

上述连续方程可用不同的变量来表达，例如以断面平均流速v（s，t）和过水断面面积A（s，t）作变量时，可以将Q=Av代入得：

注意到对棱柱形渠道有：

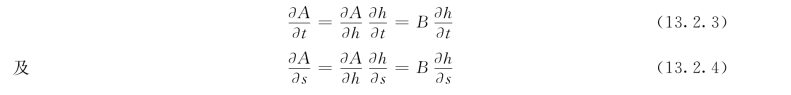
式中 B——水面宽度；

h——水深。(www.daowen.com)

将式（13.2.3）、式 （13.2.4）代入式（13.2.2）可得到以水深h（s，t）和断面平均流速v（s，t）为变量的明渠非恒定流连续方程式：

2.运动方程

明渠非恒定渐变流运动方程和有压管路非恒定渐变流运动方程在形式上是一样的，都是式（13.1.19），在考虑水头损失时为：

式中 z——水面高程，即水位。

3.圣维南方程组

由以上得到的以水深h和断面平均流速v为变量的连续方程式（13.2.5）与运动方程式（13.2.9）组合成：

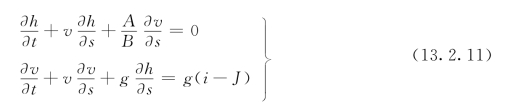
以水面高程z 及断面平均流速v 为变量的连续方程式 （13.2.8）与运动方程（13.2.10）组合成

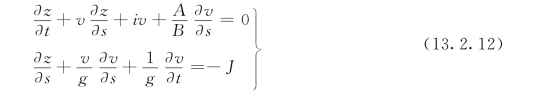
式 （13.2.11）和式（13.2.12）都称为圣维南 （Saint—Venant）方程组。在给定初始条件和边界条件的情况下求解圣维南方程组 （13.2.11）或 （13.2.12），则可得出任一时刻在任一地点的渠道水探h（s，t）和断面平均流速v（s，t）或z（s，t）和v（s，t）。