从以上的讨论中可以看到，不论是水电站还是水泵站，水击压强都是巨大的，这一巨大的压强可能导致管路变形甚至破裂。预防水击危害的措施和方法是多种多样的。例如在管路上设置消压阀。其原理是使这种阀能在压强升高时自动开启，将部分水从管中放出以降低管中流速的变化，从而降低水击增压，而当水击压强消除以后，则此阀又自动关闭起来恢复管道中水流的正常运行。此外，延长阀门的关闭时间，缩短有压管路的长度等都是减小水击压强的有效方法。设置在水电站引水系统中的调压塔就是利用缩短有压管路长度的原理来减小水击压强的一种建筑物，如图13.1.9所示，这是一个大容积的井型建筑物，当水击发生时，由阀门传来的增压波在此将反射回去，缩短了减压波回到阀门处的时间过程，从而减小水击压强，同时保护了调压塔上游的管道，使其不受水击压力的冲击。

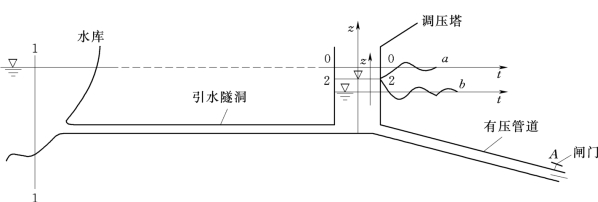
图13.1.9

调压塔中的水位在恒定流情况下，由于引水隧洞中有水头损失，因而比水库水位低一些，但也是恒定的。当A 处阀门突然关闭而产生水击现象时，由于调压塔容积比较大，它起着水库的作用，虽然塔中水位多少也会因流量变化而受到影响，但由于水击过程相对比较快，时间不太长，所以这种影响并不大。主要的是水击过程以后，由于阀门已经关闭，有压管道中流量为零（或减小流量），引水隧洞来的水流直接进入调压塔，致使塔中水位上升。与此同时，调压塔中的水位和上游库水位的差值也逐渐减小，因而引水隧洞中的水流流速也相应减小。当调压塔中水位上升到与上游库水位齐平的时候，因为惯性的缘故引水隧洞中的水流不会停止，直到调压塔中的水位高过上游库水位一定值，引水隧洞中的流速才降为零，塔中水位到达最高值。这时由于塔中水位比库水位高，所以引水隧洞中的水体将向上游倒流，塔中水位开始下降。当塔中水位降到和上游水位一样平时，由于惯性缘故这种倒流现象不会停止，直到塔水位比库水位低一定值时为止，于是产生了调压塔中水位上下波动的振荡现象，如同拉一根弹簧的过程一样。当然，由于引水隧洞及塔内水头损失等能量耗损的原因，这种振荡现象会逐渐消失，其水位变动过程如图13.1.9中曲线a所示。

以上是关闭阀门的情况，在加大阀门开度时，调压塔中水位振荡的现象也同样存在，只是塔内水体先降后升，其水位变动过程如图13.1.9中曲线b所示。

求解调压塔水面振荡的基本方程式是非恒定流连续方程和由运动方程导出的能量方程。和处理水击现象相比，不同之处是这里水的密度和引水隧洞的断面积等均作常量处理，其原因是振荡时水位变化过程比较慢而压强变化也比较小。由连续方程得调压塔、引水隧洞、有压管道间流量关系为（图13.1.10）：

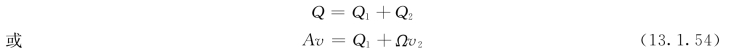
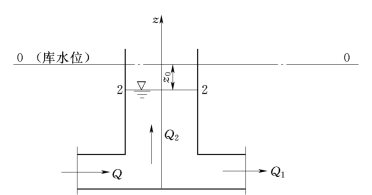
图13.1.10

式中 A——引水隧洞断面面积；

v——引水隧洞断面平均流速；

Ω——调压塔的断面面积；

v2——调压塔中的流速。

代入式（13.1.54）后得：

式中 z——调压塔水面水位；(www.daowen.com)

hi——惯性水头；

hw——水头损失。

由于调压塔断面面积比引水隧洞断面面积相对大很多，长度又相对短很多，所以调压塔中的速度水头、惯性水头和水头损失都可以忽略，则由式（13.1.56）得：

式中 L——引水隧洞长度；

ζc——引水隧洞中的水头损失系数。

在式（13.1.55）和式（13.1.57）中，只有两个未知量z（t）和v（t），在已知初始条件和边界条件下可以用差分法求出解答。

式 （13.1.55）和式（13.1.57）的差分形式为：

上式中A、Ω、Q1、g、L为已知。根据问题要求的精度确定Δt，一般取Δt=10～20s。在t=0时，隧洞中的流速v0和调压塔中的水位z0=-hw0也已知。这样，可按下述步骤进行计算：

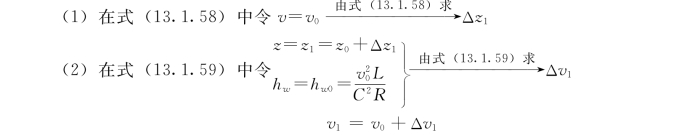
z1、v1即为t=Δt时刻的塔中水位及隧洞中流速。

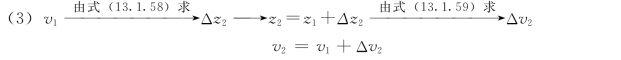
z2、v2即为t=2Δt时刻的塔中水位及隧洞中流速。

依此类推可逐时段算出3Δt、4Δt、…各时刻的塔中水位及隧洞中流速。