水击计算的主要任务是确定管道系统中的水击压强增高或降低值。

1.水击连锁方程

将式（13.1.26）及式（13.1.28）分别对t及s、s及t各进行一次微分。整理后得水击的波动方程组：

若改取s的正方向为自阀门指向上游水库，则式 （13.1.29）、式 （13.1.30）的解可写成：

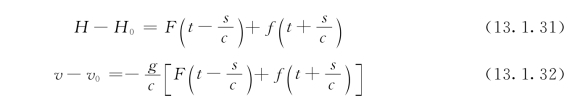
式中 H0、v0——水击发生前在恒定流时的测压管水头及断面平均流速；

H、v——水击发生后距阀门为s的断面在t时刻的测压管水头及断面平均流速；

F、f——两个未知函数，称为波函数，它们取决于管道的边界条件。

对于不计阻力的直接水击、间接水击都能用式 （13.1.31）、式 （13.1.32）在一定的初始条件和边界条件下求解。可见其F值和t1时刻s1处的F值是相同的，这样，从全管段看，就如同F波以波速c向上游传播。

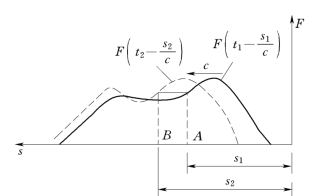
图13.1.7

同理可以说明，函数f代表以波速c由水库向阀门方向传播的压力顺波，传播过程中也不改变波形，f（t+s/c）则为t时刻通过距阀门s处断面的f波值。

所以，式 （13.1.31）、式 （13.1.32）的物理意义是：在水击过程中，t时刻坐标为s的断面处的测压管水头增值ΔH=H-H0及流速增值Δv=v-v0是同一时刻通过该断面的水击逆波和水击顺波叠加的结果。

为了得到F 和f 的具体表达式，使式（13.1.31）减式（13.1.32）得：

令式（13.1.31）加式（13.1.32）得：

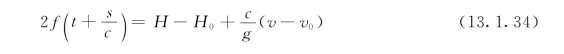
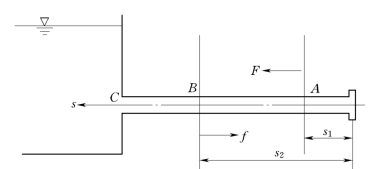
图13.1.8

因为逆波在传播过程中不改变波形，故当t2=t1+Δt，s2=s1+cΔt时，有：

即

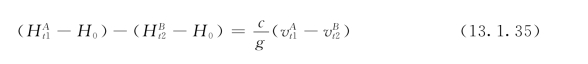
或写成

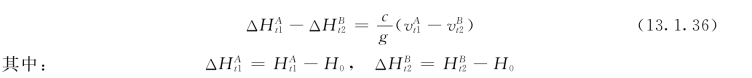
式（13.1.35）或式（13.1.36）给出了A断面在t1时刻及B断面在t2时刻的流速与水头间的关系。

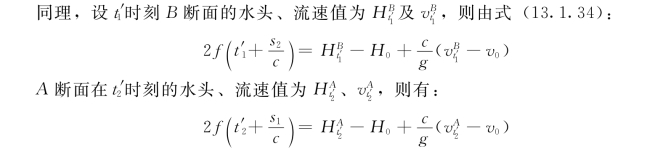
当t′2=t′1+Δt，s1=s2-cΔt时，根据顺波f不变波形的原理得：

式 （13.1.37）和式（13.1.38）给出了B断面在t′1时刻、A断面在t′2时刻的水头与流速间的关系。

联合应用方程组式（13.1.36）及式（13.1.38），即可根据已知的某断面在特定时刻的水头及流速值，求解另一断面在水击波传到的相应时刻的水头和流速。逐步推演下去就可根据已知的边界条件和初始条件求得任意断面在任意时刻的水头值和流速值。

式 （13.1.36）和式（13.1.38）称为水击的连锁方程。并且连锁方程常用下列无量纲的相对值表示：

其中：

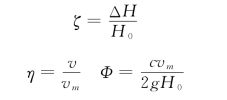
式中 ζ——水头相对增值；

η——相对流速；

vm——阀门全开时管道中的最大流速；

A、B——断面位置；

t——时间；

Φ——反映管道断面特性的无量纲数。

2.初始条件及边界条件

应用连锁方程计算水击压强时，必须首先确定其初始条件及边界条件。

（1）初始条件。所谓初始条件，就是指水击发生前 （恒定流动时）管道中的水头H0及流速v0。这可以通过恒定流的水力计算确定。

（2）边界条件。对图13.1.2的简单管道，边界条件是指上游 （管道进口断面B）及下游（管道末端断面A）的流动条件。

1）管道进口断面B的边界条件。压力管道上游一般与水库相连。由于库容很大，库水位不会因管道流量的变化而涨落。所以，上游的边界条件是：水击波的传播过程中，进口断面B的水头保持为常数，即

2）管道末端断面A的边界条件。管道末端断面与流量控制设备相连，故断面A的流动条件与控制设备的类型及其控制规律有关。但不同类型的水轮机，其流量控制设备也各不相同，所以边界条件往往比较复杂。在此，我们仅讨论一种比较简单的情况，即管道末端与一阀门相连，阀门出流类似于孔口出流，在初始条件下，其出流量可近似表示为：

相应的管道流速为：(www.daowen.com)

式中 Ω0——初始时刻阀门的开启面积；

Q0——初始时刻通过阀门的流量；

A——管道断面积；

μ——流量系数。

假定μ保持为常数，在同一水头下，阀门全开（Ω=Ωm）时通过的最大流量为：

相应的管道流速为：

对水击发生后的任意时刻t，设阀门的开启面积为Ωt，管道末端断面A的水头为H At，则通过阀门的流量为：

A断面的相应流速：

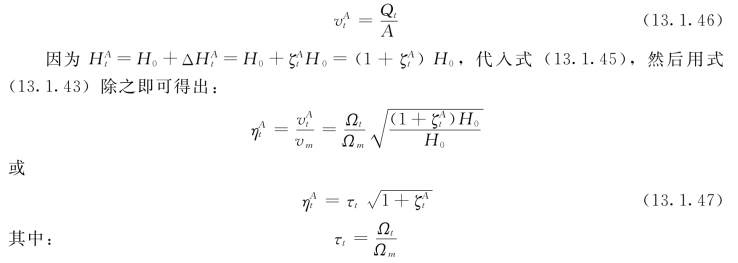
式中 τt——相对开度。

上式即为管道末端断面A的边界条件。当已知开度随时间的变化规律τt=f（t）时，由该式即可求得任意时刻t、A断面的相对流速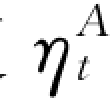 与相对水头增值量 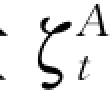间的关系。

必须指出，末端断面A的边界条件式（13.1.47）主要适用于以针型阀控制流量的冲击式水轮机。对于反击式水轮机，其流速变化不仅与导水叶开度及水头有关，而且还与转速有关，其边界条件必须由水轮机特性曲线确定，故对反击式水轮机而言，式 （13.1.47）只是一种粗略的近似关系。

3.连锁方程的应用

结合初始条件和边界条件应用连锁方程式（13.1.39）和式（13.1.40）即可求解水击问题。

若以相（t=Tr=2l/c）作为时间的计算单位，A断面产生的水击波，经l/c即半相时间传至上游进口B断面处，再经过半相时间反射波又回至A断面处，令t1=0表示水击开始前的初始时刻，则t2=0.5相 （记作t2=0.5）为A断面的水击波到达B 断面所需的时间，根据连锁方程式（13.1.39）有：

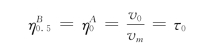
τ0为阀门初始相对开度，从t=0.5相开始，水击波从B断面向下游反射，至t=1.0相时到达A断面，应用连锁方程式（13.1.40）有：

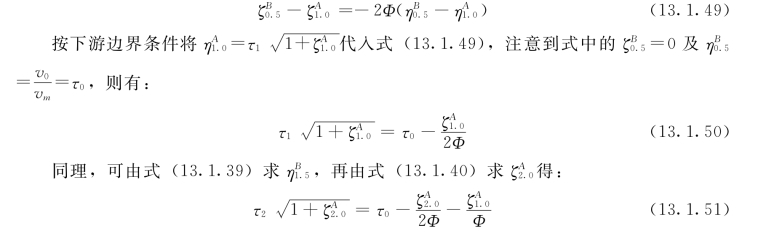
这样连续推演下去，可求得阀门关闭完毕的第n相末A 断面的水头相对增值的表示式为：

由于水击波从A断面发生到反射回来的时间为一相，所以一般讲A断面水击压强在每相之末变幅最大，因此只要算出A断面在各相末的水击压强值，即可求得最大水击压强增高值及水击压强降低值。也即由式（13.1.52），令n=1，2，…则可求得A断面在关闭阀门过程中的最大压强增高值。

对于直接水击，式 （13.1.52）仍是适用的，这时因阀门在第一相末已全部关闭，故令式（13.1.50）中的τ1=0，得：

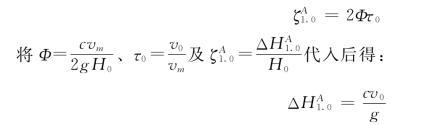
这正是直接水击的压强水头计算式（13.1.9）。

式 （13.1.52）不仅对关闭阀门的情况适用，同时也适用于开启阀门的情况。不过，当开启阀门时，A断面会产生压强降低，为方便起见，改变一下式 （13.1.52）的表达方式。令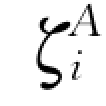=-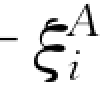，代入式（13.1.52）得：

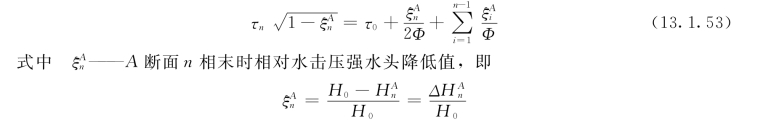
例13.1.1 某水电站引水钢管，管材弹性模量E与水的体积模量K 之比为100∶1，管长l=580m，管径D=2400mm，管壁厚度δ=20mm，作用水头H0=180m，阀门全开时管中流速vm=2.8m/s，阀后为大气压强。试求下列情况下阀门处管中第一相末时的压强水头。

（1）初始开度τ0=1，终了开度τ=0，阀门关闭时间Tz=1s。

（2）初始开度τ0=1，终了开度τ=0，阀门按线性方式改变开度，Tz=2.49s。

（3）初始开度τ0=0，终了开度τ=1，Tz=1s。

解：

按薄壁钢管水击波传播速度公式：

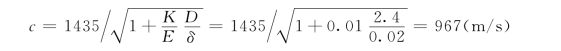
相长：

（1）当阀门由τ0=1关至τ=0时，阀门关闭时间Tz＜2l/s，故为直接水击，由阀门开始的水击波传到水库后反射，反射的减压波尚未到达阀门时阀门已完全关闭，因此直到第一相末减压波回到阀门处为止，水击压强一直维持不变，故可按第一相末公式计算其水击压强：

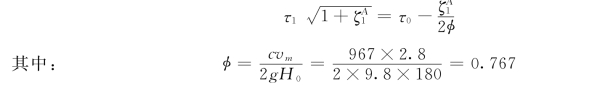
因τ1=0，τ0=1，代入上式得：

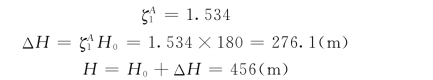
（2）首先应决定第一相末的阀门开度，因阀门开度是按线性变化的，故

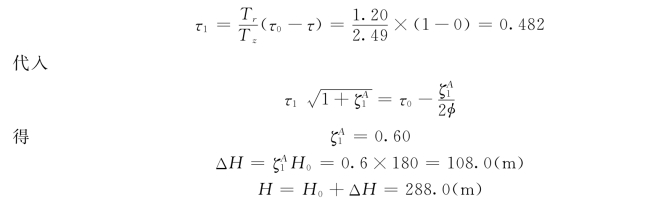
（3）当τ0=0，τ1=1时，这是阀门开启的情况，可应用公式 （13.1.53）计算第一相末水击压强：

代入τ0=0，τ1=1后得：

所以

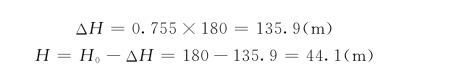
可见，阀门开启时的水击压强是负的。