1.波的能量
不可压缩液体在重力作用下所产生的波浪,其能量是由各个液体质点运动时的动能及因波动而使液体重心较平衡位置升高所产生的势能而组成的。
波浪运动中任一水质点具有的合速度可用流速势函数表示为:
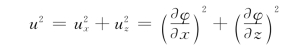
那么,在一个波长范围内具有的单位宽度(液体厚度)的动能为:
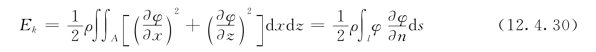
式中 l——液体的周界;
n——周界的外法线;
A——一个波长范围内的断面面积。
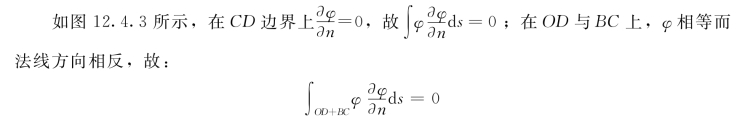
在OAB上,Oz为外法线方向。
![]()
(1)在浅水推进波情况下:
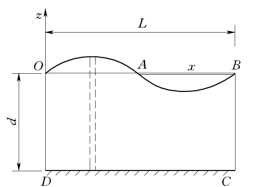
图12.4.3
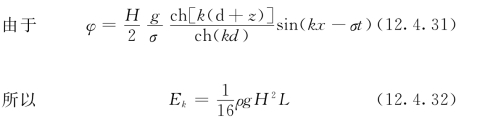
(2)在无限水深情况下,可得与式 (12.4.32)相同的结论。
下面考虑在一个波长之内所具有的势能。设一竖直(垂直于Ox轴)的底面积为d x·1的柱体液块,它在Ox轴上面的体积为ηd x,其质量为ρηd x,重心高度为η/2,故一个波长之内的势能为:
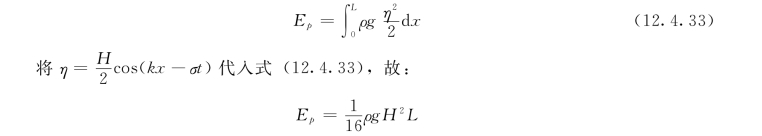
这样波浪在一个波长内具有单宽能量为:
![]()
2.波能量的传递
现在来具体研究一下波能是如何传递的。推进波的水质点在波动时虽然没有向前移动,但波能却随着水质点的运动而顺着波浪传播方向向前传递,如图12.4.4所示。取一垂直于波浪传播方向的平面AB,设波浪自左向右传播,每一个穿越平面AB的水质点在一个波周期内必将两次通过这个平面,一次自左向右流出,一次自右向左流入,若波浪为深水推进波,那么水质点在波动时具有的动能是常数,流出、流入AB平面时的动能是相等的。由于流出AB平面时的位置M1点总是高于流入时位置M2,因此水质点以较大的势能流出AB平面而以较小的势能流入此平面。这样水质点每一个波周期内,就有一部分势能留在这个平面的右侧,波能就不断地通过水质点的运动向前传递,这种现象就叫波能传递。单位时间内波能的传递量称为波能流量,记为Φ。(https://www.daowen.com)
设
![]()
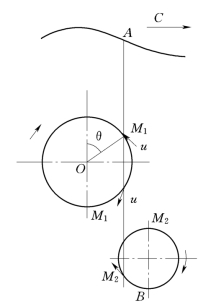
图12.4.4
式中 n——波能传递率。

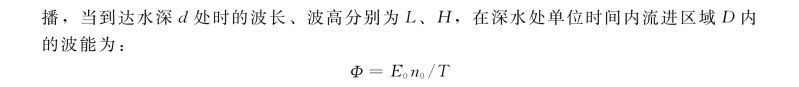
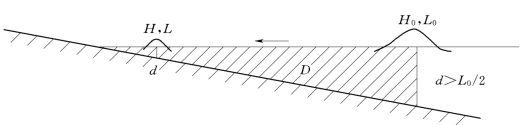
图12.4.5
在浅水处单位时间内流出区域D的波能为:
![]()
假设波周期在波浪传播过程中保持不变,且不考虑波能的损失。
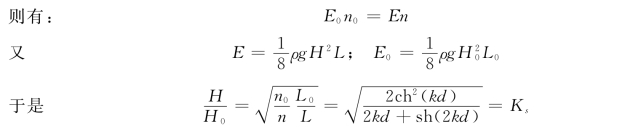
式中 Ks——波高的浅水系数。
图12.4.6为不同水深条件下的波浪特性的示意图。
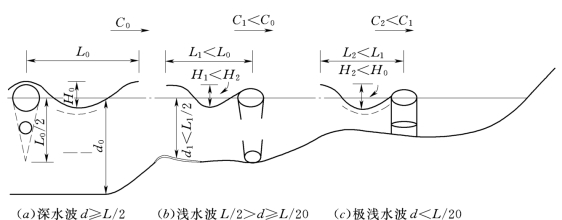
图12.4.6
例12.4.3 在例12.4.1的条件下,试求单位宽度水体的波能流量Φ。
解:
由例12.4.3解得C=6.5m/s,L=32.5m,且已知:d=6.2m,H=1.2m,故波能流量为:
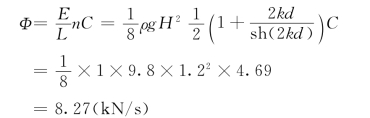
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





