立波是两组波浪要素完全相同而方向相反的推进波叠加后产生的波动现象，立波的特点是水面只在原处起伏振动，波形并不向前推进。例如，当推进波遇到和前进方向正交的直立壁面而反射时，反射波与原来推进波叠加即可产生立波。微幅势波既然有流速势存在，按照势流叠加原理，产生的合成运动仍然是有势的。叠加后合成的流速势等于原来各个运动流速势之和，即立波的流速势函数可用两个方向相反而大小相等的推进波流速势函数叠加而得：

以有限水深推进波为例，其流速势函数φ1 为：

其反射波的流速势函数φ2 可设为：

叠加后的合成流速势函数为：

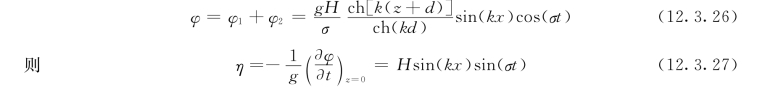
式中 H——原来推进波的波高。

由式（12.2.69）可见，对于给定时刻t，可改写成为：

图12.3.1

这个立波质点的运动轨迹也可由式（12.3.26）的合成流速势函数来推求，其结果为：

式中 x0、z0——质点初始位置的坐标。(www.daowen.com)

故立波的质点轨迹是与Ox成倾角的直线，其斜率决定于质点的初始位置，如图12.3.2所示。

图12.3.2

在立波的节点上，水质点沿水平方向振动；在波腹中间，水质点沿垂直方向振动。

解：

由题意可知，反射后的波动，其波浪要素与入射波完全相同，但传播方向相反，因此速度势应为：

由势流叠加原理得：

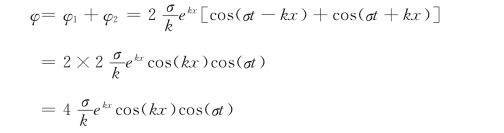
波动自由表面方程：

注意到φ1、φ2 为深水推进波，σ2=kg，故有：