1.边界条件
对于二维规则波浪问题,求解式(12.2.10)时应考虑表面和水底处的边界条件。在自由表面上具有动力学的和运动学的两种边界条件
(1)动力学边界条件:现采用符号η表示任意断面上波浪表面超出静水位的高度,η=η(x,t),在自由表面上(图12.1.4),z=η(x,t),此处有:
![]()
因此,由式(12.2.13)可以得到:
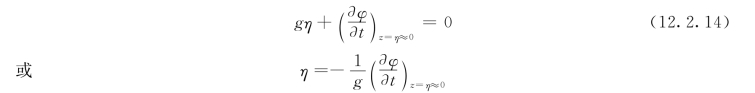
(2)运动学边界条件:
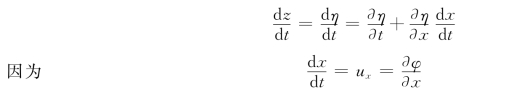
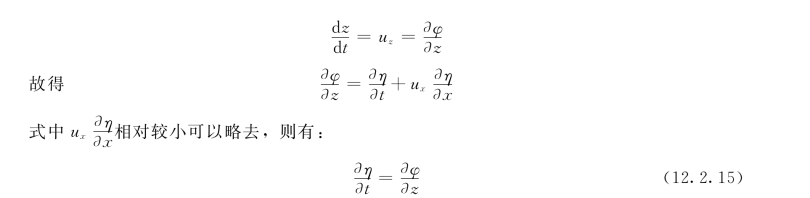
将式(12.2.14)对t求导可得到:
![]()
比较式(12.2.15)、式 (12.2.16)得:
![]()
在式(12.2.14)~式 (12.2.17)中,脚标z=η≈0表示该值是自由表面处的值,即z=η处应满足的条件,但由于研究的是微幅波,故η≈0,也即在计算中可以认为在z=0(即原静水位)处满足上述条件,这就使问题简化多了。
在海底处,液体质点只有平行底面方向的速度,而法向速度为零。设位于d处的底面是水平且不透水的,则上述条件为:
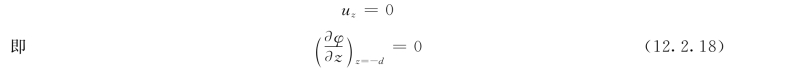
在深海情况时,d→∞,式 (12.2.18)将有下列形式:
![]()
2.初始条件(https://www.daowen.com)
令瞬时力作用终止时的瞬间为初始时刻,设此时刻为t=0。若所研究的波浪运动波高较小,在自由表面上,可认为z=η≈0,由于引起波浪运动的初始压力应已知,因此,根据式(12.2.7)(假设为二维问题):
![]()
式中 f1(x)——已知函数。
此外,初始压力将引起某些初始扰动,而自由表面的初始位置应与这种扰动相适应,即当t=0时:
![]()
由条件式(12.2.14)得:

为了确定问题的解答,式 (12.2.20)、式 (12.2.21)中f1(x)、f2(x)应为已知函数。
综上所述,求解波浪运动中的流速势函数φ应当满足拉普拉斯方程及相应的边界条件和初始条件。
(1)拉普拉斯方程:

(2)边界条件:
自由表面上(对微幅波,z=η≈0):

在水平底面上:
![]()
(3)初始条件:
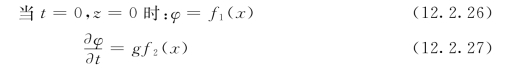
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





