波浪是海洋中最常见的现象之一，是岸滩演变、海港和海岸工程最重要的动力因素，其作用力是设计防波堤、码头、闸门、进水塔和采油平台等建筑物时必须考虑的外力之一。因此，研究波浪理论对国民经济许多部门都有重大意义。

波浪是一种波动现象，是一种水质点振动与传播的现象。波浪可分类如下。

（1）按水质点所受的主要恢复力可分为重力波、表面张力波、潮汐波等。

（2）按干扰力或发生的原因可分为风成波、地震波、船行波等。

（3）按引起波动的力在波浪形成后是否仍持续作用可分为强迫波、自由波。

（4）按波动时水质点移动的性质可分为振荡波和推移波。振荡波又分为推进波和立波。推进波是质点基本上围绕其静平衡位置沿着封闭的或接近封闭的轨迹运动，比如风成波；立波是原始推进波和反射波叠加后生成的波，也称为驻波。推移波是质点有明显的位移，比如潮汐波、地震波和洪水波等。

（5）按波动传播的性质可分为二维波和三维波。

（6）按波浪的几何尺寸可分为短波和长波。

（7）按水域底部是否对波浪有影响可分为深水波与浅水波。

（8）按波浪要素是否随时间改变可分为规则波和不规则波。

此外，根据波浪运动的运动学和动力学处理方法，还可把波浪分为微小振幅波和有限振幅波两大类。所谓微小振幅波（简称微幅波）是指波陡较小的波。研究微幅波时应用了线性化理论，比较简要明确。随着振幅的增加，波动的非线性效应就变得显著起来，问题也变得复杂了，因而出现了各种研究非线性有限振幅波的方法和理论，但微幅线性波仍然是研究这些有限振幅波的基础。由于微幅波得出的微分方程是线性的，有限振幅波得出的微分方程是非线性的，故有时也分别称为线性波和非线性波。

当研究波浪现象时，首先必须了解波浪的几何特征与运动特征。描述波浪运动性质及其形态的各主要物理量，如波长、波高、波速等，称为波浪要素，如图12.1.1所示。现将波浪的主要要素定义如下：

（1）波峰：在静水面以上的波浪部分。

（2）波谷：在静水面以下的波浪部分。

（3）波峰顶：波峰的最高点，简称波顶。(www.daowen.com)

（4）波谷底：波谷的最低点，简称波底。

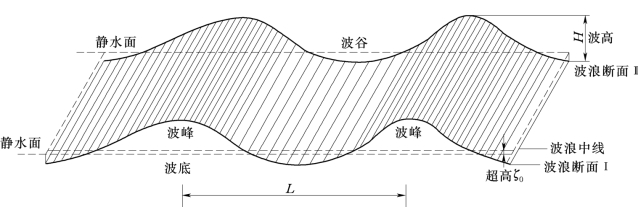
图12.1.1

（5）波峰线：垂直波浪传播方向上各波峰顶的连线。

（6）波向线：与波峰线正交的线，即波浪传播方向。

（7）波高：相邻波峰顶与波谷底间的垂直距离，通常以H 表示，单位以m计。在我国台湾海峡曾记录到波高达15m的巨浪。

（8）波长：两相邻波峰顶（或波谷底）间的水平距离，通常以L表示，单位以m计。海浪的波长可达上百米，而潮波的波长可达数公里。

（9）波陡：波高与波长之比（H/L）。海洋上常见的波陡范围为1/30～1/10。波陡的倒数称为波坦。

（10）周期：波浪起伏一次所需的时间，或相邻两波峰顶通过空间固定点所经历的时间间隔，或波峰顶或波谷底向前推进一个波长所需要的时间。通常以T 表示，单位以s计。在我国沿海波浪周期一般为4～8s，曾记录到周期为20s的长浪。

（11）频率：单位时间内的波动次数，数值上等于波浪周期的倒数。

（12）波速：波形沿水平方向移动的速度。通常以C表示，它等于波长除以周期，即C=L/T，单位以m/s计。

（13）波浪中线：等分波高的水平线，此线一般在静水面以上，其超出的高度称为超高。一般由于波峰比较尖突，波谷比较平坦，静水面至波峰的距离大于静水面到波谷的距离，因此波浪中线位于静水面之上。

波浪剖面（波形、波面）z=f（x），如图12.1.2 （a）所示。

波浪过程线z=f（t），如图12.1.2 （b）所示。