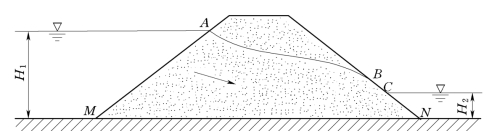
【摘要】:应用上述的拉普拉斯方程求解渗流问题时,还需给出该问题的初始条件和边界条件。初始条件是指初始时刻整个渗流域内各点的渗透流速和渗透压强。对于如图11.6.2所示的土坝,边界条件如下。
应用上述的拉普拉斯方程求解渗流问题时,还需给出该问题的初始条件和边界条件。
初始条件是指初始时刻整个渗流域内各点的渗透流速和渗透压强。对于非恒定渗流才有初始条件,对恒定渗流不需要初始条件。
对于如图11.6.2所示的土坝,边界条件如下。
1.不透水边界
不透水边界指不透水岩层或不透水的建筑物轮廓,如图11.6.2中的MN 为不透水边界,沿该边界法线方向的渗透流速un=0即
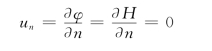
2.透水边界
透水边界是指水流渗入和渗出的边界,如图11.6.2中的AM 和CN。上述透水边界上各点的水头值H 相等,是一条等水头线 (或等势线)。在AM 上,φ=-k H1;在CN上,φ=-k H2。
 (https://www.daowen.com)
(https://www.daowen.com)
图11.6.2
3.浸润面边界
浸润面即是地下水的自由表面,如图11.6.2中的AB所示。浸润面上的压强等于大气压强,即p=0;其各点水头H=y,不是常数,所以浸润面不是等水头面。在浸润面上,垂直于该面的渗透流速un=0,即
![]()
故浸润面是流线组成的流面,浸润线是一条流线。
4.溢出段边界
由于浸润线出口高于下游水位,故形成溢出段,如图11.6.2中的BC。溢出段的压强为大气压强,即p=0;溢出段各点水头H=y,水头随高程而变。溢出段是流线终点的连线,它不是等势线,也不是流线。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章






