土坝的坝体结构型式及地基条件有多种情况，如坝体有均质的、带心墙的、带斜墙的、设排水的；地基可有透水的和不透水的等。其中最简单的是不透水地基上的均质土坝，它的渗流情况是研究其他型式土坝渗流的基础。

凡是地基的渗透系数小于坝体土壤渗透系数的1%的，都可认为是不透水地基。

设有水平不透水地基上的均质土坝，其剖面如图11.5.1所示。当上游水深H1和下游水深H2固定不变时，渗流为恒定流。水流通过上游边界AM 渗入坝体，在坝内形成无压渗流。因克服阻力，渗流不断损失能量，水头不断下降，其自由表面AB即为浸润线。在下游坝坡，一部分渗流沿BC渗出，BC称为溢出段，B点称为溢出点，BC两点之间的垂直距离以a0表示，a0称为溢出高度。另一部分则通过CN 流入下游。

图11.5.1

为什么存在溢出段BC呢？其原因可说明如下：下游坝坡CN 在下游水面以下，其各点总水头是个常数，故CN 是一条等势线。若B点不在C 点之上而与C 点重合，如图11.5.2所示。因浸润线本身是一条流线，故必与下游坝坡CN （等势线）正交，并形成如图11.5.2中EC所示的形状。但浸润线就是总水头线，只能沿程下降而不能上升，像EC那样升起是不可能的，所以B点的位置必然在C 点以上，而形成溢出段。浸润线在溢出点处与下游坝坡相切。

土坝平面渗流问题，常采用分段方法进行计算。一般有三段法和两段法两种方法，下面仅对两段法详加介绍。以图11.5.1中的土坝渗流为例，两段法中的第一段用矩形体AA′M′D 代替三角体AMD，该矩形体宽度λH1的确定应满足下列的条件：在相同的上游水位H1和单宽渗流量q的情况下，通过矩形体和三角体到达通过上游坝肩的1-1断面时的水头损失a相等。根据试验研究，设等效的矩形体宽度为λH1，λ值可由下式确定：

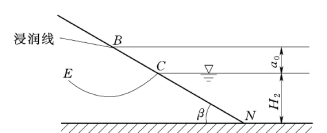
图11.5.2

式中 m1——土坝上游的边坡系数。

这样，整个渗流区就由两段组成，第一段为AA′M′EB，第二段为BEN。

1.上游段的计算

设水流从A′M′面入渗，将上游段看作无压渐变渗流，A′M′为入流断面，该断面上的水头为H1，BE为该段最后一个过水断面，断面上的水头为（a0+H2）。渗流从A′M′断面至BE 断面的水头差为H1- （a0+H2），两断面间的渗流路径长可近似等于L+λH1-m2（a0+H2），m2为土坝下游的边坡系数。根据平底坡渐变渗流浸润线公式 （11.3.7），通过此段的单宽渗流量为：

由于a0未确定，故不能由上式直接计算q，还需通过对下游段的分析，再建立一个包括未知数a0和q的方程。

2.下游段的计算

下游段BEN 如图11.5.1所示，这一段上游面BE的水深为a0+H2，也就是BE上各点的水头值均为a0+H2。下游边坡BN 分为两段：BC段在下游水位以上，CN 段在下游水位以下。因此，下游段可分为两部分：下游水位以上部分为Ⅰ区和下游水位以下部分为Ⅱ区，每一流区内的流线都近似地设为水平线。设z轴原点为B，垂直向下为正，如图11.5.3所示。

图11.5.3

在Ⅰ区，任一水平流线的水头损失应等于该流线至浸润线末端溢出点B的垂直距离z，而流线长度为m2z，所以Ⅰ区任一元流的单宽渗流量为：

Ⅰ区的单宽渗流量q1等于d q从z=0到z=a0的积分，即：

在Ⅱ区，下游边坡CN 各点水头均等于H2，所以任一条流线的水头损失均等于（a0+H2）-H2=a0，流线长度则等于m2z，故下游段的单宽渗流量为：

(www.daowen.com)

联立求解式（11.5.2）和式 （11.5.3），可求得土坝的单宽渗流量q和溢出高度a0。求解时可用试算法。

土坝的浸润线方程可采用平底坡无压渐变渗流浸润线式 （11.3.7），以图11.5.1为例，设距假想的矩形体上游坝面的距离为x断面水深为y，则按式（11.3.7）可写为：

设一系列y值，即可算得一系列对应的x值，绘成浸润线A′B。但实际浸润线应从上游坝面A点开始，并在A点垂直于坝面AM。将x=λH1+m1d代入式（11.5.4）求得断面1-1处的水深为h，并得到F点，然后用手描法连接AF，使之成为一条平顺光滑曲线，这就是实际的浸润线，如图11.5.1所示。

例11.5.1 有一水平不透水层上的均质土坝，坝高为19m，上游水深H1=16m，下游水深H2=4m，上游边坡系数m1=3，下游边坡系数m2=2，坝顶宽度b=12m，渗透系数k=2×10-4cm/s。试求上坝单宽渗流量q，下游坝面溢出高度a0及1-1断面处的水深h。

解：

两段法计算：矩形等效体宽度

代入式（11.5.2）得：

代入式（11.5.3）得：

假定一系列a0值，分别求得对应的f1（a0）、f2（a0）的值，见表11.5.1。

表11.5.1

绘出f1（a0）、f2（a0）与a0的关系曲线，如图11.5.4所示。由两曲线的交点得：

由式（11.5.4）得：

图11.5.4

1-1断面处x为：

（x为距假想的矩形体上游坝面的距离）此例上式中h=H1。