为了增大抽水量，或者为了更有效地降低地下水位，在不太大的范围内有几口井同时工作。由于各井间距不大，各井的渗流互有影响致使地下浸润面变得复杂。这些井就称为井群，如图11.4.3所示。

井群所形成的渗流场，可以看成每个单井所形成的渗流场的叠加。如果能够找到单井的流速势函数，根据势流叠加原理，就可以找到井群的流速势函数，从而可以解决井群的渗流计算。为此，我们首先需要求出单井的流速势函数。

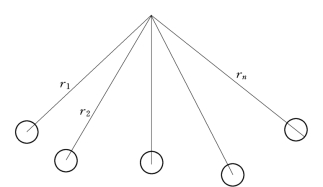
图11.4.3

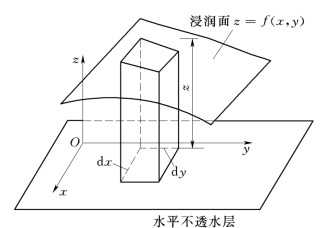
图11.4.4

设含水层下有一水平不透水层，取x、y轴在水平不透水层上，z轴垂直向上，如图11.4.4所示，则无压渐变渗流的浸润面方程为：

式中 z——浸润面的高度。

根据杜比公式（11.3.1），可得无压渐变渗流的运动方程为：

式中 ux、uy——铅垂线上任一点的渗流流速在x、y方向的分量；

vx，vy——铅垂线上平均渗流流速在x、y方向的分量；

H——铅垂线上任一点的水头，等于浸润面高度z。

式 （11.4.5）也可写为：

下面推导渐变渗流的连续方程。取图11.4.4上所示d x d y为底面、高为z的柱体为控制体。对于恒定流，连续方程式（3.4.3）为：

上式表明单位时间内流出与流入控制体表面的质量差为零。故单位时间x方向通过控制体表面流出与流入的质量差为：

同理，单位时间y方向通过控制体表面流出与流入的质量差为：

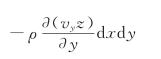
由式（3.4.3），得：

这就是无压渐变渗流的连续方程。

将式（11.4.6）代入该式，得：

由该式可知，在水平不透水层上的无压渐变渗流，z2满足拉普拉斯方程。因此可以把z 2看作无压渐变渗流的流速势函数。设zi为某单井单独作用时的某点的水位，z为井群中某点的水位，则各单井的流速势函数z 2i叠加可以得到井群的流速势函数z 2。(www.daowen.com)

由式（11.4.1）可知，单井的浸润线方程为：

则井群的浸润线方程为：

若令各单井出水流量Qi均相同，井群总出水流量为Q0，则Qi=Q0/n，代入上式并展开得：

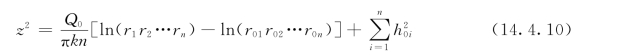
在井群中也引入影响半径的概念，一般井群的影响半径R远大于井群的尺度，故可近似认为在影响半径处r1≈r2≈…≈rn≈R，该处水位z=H，则

将式（11.4.11）与式（11.4.10）相减，得：

经整理得完全普通井群地下水位的计算公式为：

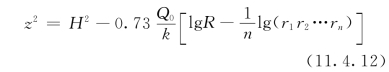
利用该式可求出井群中任一点的浸润线高度，也可反求出井群的出水流量Q0。

例11.4.1 为了降低某建筑物基础施工场地的地下水位，在基坑现场布置了8个普通完全井，呈矩形布置如图11.4.5所示。已知矩形边长为60m和40 m，每口井抽水量为5L/s，井群的影响半径R=500m。含水层深度H=10m，渗透系数K=0.001m/s，试求井群中心点O的地下水位z。

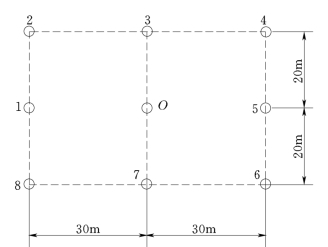
图11.4.5

解：

由井群浸润线方程式（11.4.9）

计算井群中心O点的地下水位z。

已知H=10m，Q0=8×5L/s=40L/s=0.04m3/s

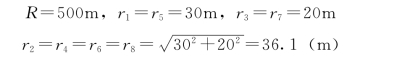
代入上式，得：

井群中心O点的地下水位z为8.01m，比原地下水位降低了将近2m。

注：在该题中，若求某单井井中水位zi，也可利用井群浸润方程式 （11.4.9）计算，但这时要注意该井ri=r0i，即以该井的半径r0i代入ri，其他各ri仍为各井中心至该井中心的距离。