水平不透水层上的完全普通井如图11.4.1所示，原地下水位线如虚线所示。设原地下水深度为H，井的半径为r0，当不吸取地下水时，井中水位与原地下水位齐平。当从井中吸取流量时，井中水位下降，四周地下水汇入井中并形成漏斗形的浸润面。若吸取的流量不大且为恒定时，经过一段时间，井四周的渗流可认为达到恒定状态。井中水位下降值s和漏斗形浸润表面的位置均保持不变。

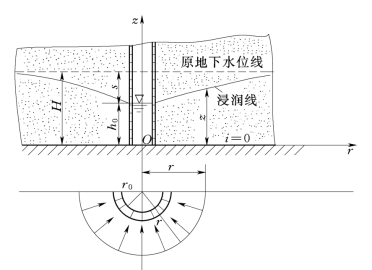
图11.4.1

井周围的渗流运动，严格来说属于三元渗流，但这样求解相当复杂。我们可以这样简化：在均质各向同性土壤的地层中，井周围渗流的过水断面应是以井中心为圆心、r为半径的一系列圆柱面。渗流对井中心是轴对称的，即任一径向断面上的渗流情况都是相同的，除井壁附近区域外，流线近似于平行，因此，渗流可以近似看作是一元渐变渗流，而且符合达西定律，可以运用杜比公式进行计算。

设z为距井中心为r处的浸润线高度，按一元渐变渗流的杜比公式 （11.3.1），半径为r处的断面平均流速v为：

过水断面为以r为半径的圆柱面，即A=2πrz，则井的渗透流量为：

分离变量并积分得：

利用r=r0时z=h0的条件，可得：

(www.daowen.com)

式中h0和r0分别为井中水位和井的半径。式 （11.4.1）为完全普通井的浸润线方程式。利用该式可计算该井任意位置r处的浸润线高度z。

浸润线在离井较远的地方，逐步接近原来地下水位。在井的渗流计算中，常引入一个假定：即认为抽水的影响只限于影响半径R以内。在影响半径以外的区域，原地下水位不受影响，即当r=R时，z=H （H 为原地下水位），则完全普通井的出水量公式为：

从该式可看出：当k、r0、R、H 一定时，抽水量Q愈大，井中水位h0愈低。

将水注入的井称为注水井，用于回灌地下水和测定水文地质参数，此时出水量为负值，仍可应用上式计算。井的影响半径需要用实验方法或根据经验来确定。在初步计算中可采用下面的经验数值：细砂R=100～200m，中砂R=250～500m，粗砂R=700～1000m。也可采用如下的经验公式计算：

式中 s——井中水位下降的高度；

k——渗透系数，以m/s计；

其余均以m计。

井的影响半径R是近似的，用不同方法得出的R值差别也较大。但因流量与井的影响半径的对数值成反比，所以影响半径的差别对流量值的影响并不大。