一元渐变渗流的浸润线和明渠水流一样，也可分为降水曲线和壅水曲线。但因渗流流速水头忽略不计，浸润线就是总水头线，因此浸润线上各点高程总是沿程下降的。由于渗流流速极其微小，因此临界水深在渗流中已失去意义，故一元渐变渗流中只有正常水深，没有临界水深。因而浸润线分区也只有两个区，即N N 线以上的a区和N N 线以下的b区。下面对各种底坡的浸润线分别加以讨论。

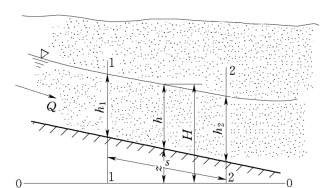
图11.3.2

1.正底坡 （i＞0）

如图11.3.3所示，对正底坡，可以发生均匀渗流。若渐变渗流为均匀流动，则水深沿程不变，即h=h0，h0称为均匀渗流的正常水深，由于d h/d s=0，根据式（11.3.2）可知，均匀渗流的单宽渗流量为：

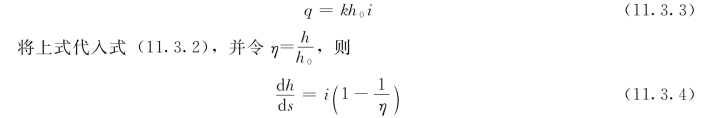
又因d h=h0dη，则式（11.3.4）可写为：

把上式从1-1断面到2-2断面进行积分，得：

式中s为1-1断面至2-2断面的距离。该式可用来计算正底坡非均匀流时的浸润线。

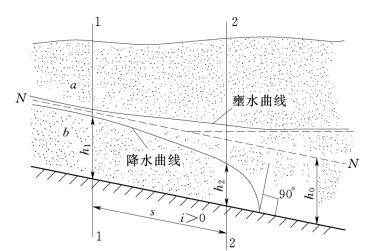
图11.3.3

正底坡渐变渗流浸润线有两种形式，如图11.3.3所示。

在a区，由于η＞1，由式 （11.3.4）可知，d h/d s＞0，浸润线为壅水曲线。当h→h0时，d h/d s→0，即浸润线在上游以N N 线为渐近线。当h→∞时，d h/d s→i，即浸润线在下游以水平线为渐近线。

在b区，由于η＜1，可知d h/d s＜0，浸润线为降水曲线。当h→h0时，d h/d s→0，浸润线在上游以N N 线为渐近线。当h→0时，d h/d s→-∞，即浸润线将与不透水层基底正交，但这时已不是渐变渗流，不能应用式（11.3.4）分析，即浸润线水深在下游不会趋于零，而是以某一水深溢出渗流域，这个水深取决于具体边界条件。

2.平底坡 （i=0）

平底坡渐变渗流浸润线，如图11.3.4所示。此时式（11.3.2）将为：

从1-1断面至2-2断面积分，可得：

利用该式可计算平底坡的浸润线，该浸润线为二次抛物线。由式（11.3.6）可知，平底坡浸润线只有一种形式，即降水曲线。当h→0时，d h/d s→-∞，即浸润线将与不透水层基底正交，但这时已不是渐变渗流，式 （11.3.6）分析的已不适用。与正底坡一样，在渗流下游浸润线是以某一水深溢出渗流域。

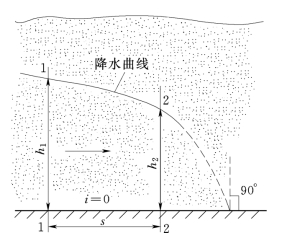
图11.3.4

(www.daowen.com)

图11.3.5

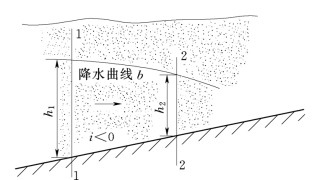
对于反底坡（i＜0），渐变渗流也只有一种浸润线，即降水曲线，如图11.3.5所示。在浸润线上游当h→∞时，d h/d s→i，即浸润线上游以水平线为渐近线；在下游，浸润线仍是以某一水深溢出渗流域。此种情况下的浸润线如下式：

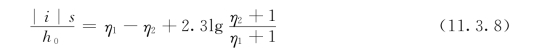
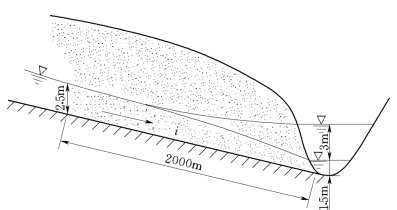
图11.3.6

例11.3.1 某河道左岸为一透水层，如图11.3.6所示，其渗透系数k=2×10-3cm/s，不透水层底坡i=0.002，修建水库之前距河道2000m处的水深为2.5m，河中水深为1.5m，若在此河道下游修建水库，河中水位抬高3m，若该断面处水深不变，试问建水库后单位宽度渗透流量将减少多少？

解：

未建水库之前，浸润线为降水曲线，渗入河中的流量可按式 （11.3.5）求得。式（11.3.5）两边同乘以h0，得：

代入已知数据并化简得：

采用试算法求得渐变渗流的正常水深h0。

表11.3.1　 h0f （h0）关系表

内插取h0=2.684m，由式（11.3.3）可得渗入河渠中的单宽渗流量为：

修建水库以后，下游水位壅高，浸润线为壅水曲线，h2=4.5m，将其代入式（11.3.5），化简得：

采用上述试算方法求得h0=1.66m，由式（11.3.3）可得壅水后渗入河渠中的单宽渗流量为：

壅水后的渗流量较未建库前的渗流量减少了：